naiva Bayes är en probabilistisk algoritm som vanligtvis används för klassificeringsproblem. Naiva Bayes är enkel, intuitiv, och ändå fungerar förvånansvärt bra i många fall. Till exempel, skräppostfilter e-app använder bygger på naiva Bayes. I den här artikeln ska jag förklara rationalerna bakom naiva Bayes och bygga ett spamfilter i Python.,y, I’ll focus on binary classification problems)

Before we get started, please memorize the notations used in this article:
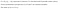
Basic Idea
To make classifications, we need to use X to predict Y., Med andra ord, med tanke på en datapunkt X=(x1,x2,…,xn), vilken udda av Y är y. detta kan skrivas om som följande ekvation:

detta är den grundläggande idén om naiva Bayes, resten av algoritmen är verkligen mer fokus på hur man beräknar den villkorliga sannolikheten ovan.
Bayes teorem
hittills har Mr Bayes inget bidrag till algoritmen. Nu är hans tid att lysa., Enligt Bayes teorem:

detta är en ganska enkel omvandling, men det överbryggar klyftan mellan vad vi vill göra och vad vi kan göra. Vi kan inte få P(Y|X) direkt, men vi kan få P(X|Y) och P(Y) från träningsdata., Here’s an example:

In this case, X =(Outlook, Temperature, Humidity, Windy), and Y=Play., P(X|Y) och P(Y) kan beräknas:

<|div>
naiv Bayes antagande och varför <|h2>
teoretiskt är det inte svårt att hitta p(x / y). Det är dock mycket svårare i verkligheten när antalet funktioner växer.,


Having this amount of parameters in the model is impractical., För att lösa detta problem görs ett naivt antagande. Vi låtsas att alla funktioner är oberoende. Vad betyder det här?,div>



This is a big deal., Vi ändrade antalet parametrar från exponentiell till linjär. Detta innebär att naiva Bayes hanterar högdimensionella data väl.
kategoriska och kontinuerliga funktioner
kategoriska Data <|p>
för kategoriska funktioner är uppskattningen av P(Xi / Y) lätt.,

ett problem är dock att om vissa funktionsvärden aldrig visar (kanske brist på data) kommer sannolikheten att vara noll, vilket gör hela den bakre sannolikhetsnollen noll., Ett enkelt sätt att åtgärda detta problem kallas Laplace Estimator: lägg imaginära prover (vanligtvis en) till varje kategori

kontinuerliga data
för kontinuerliga funktioner finns det i huvudsak två alternativ: diskretisering och kontinuerliga naiva Bayes.
diskretisering fungerar genom att bryta data i kategoriska värden., Den enklaste diskretiseringen är likformig binning, vilket skapar lådor med fast intervall. Det finns naturligtvis smartare och mer komplicerade sätt som rekursiv minimal entropi partitionering eller SOM-baserad partitionering.

det andra alternativet använder kända distributioner.,

det finns naturligtvis andra distributioner:

även om dessa metoder varierar i form, är kärnidén bakom densamma: förutsatt att funktionen uppfyller en viss fördelning, uppskattar parametrarna för distributionen och sedan får den sannolikhetsdensitetsfunktion.,
styrka och svaghet
- även om det naiva antagandet sällan är sant, fungerar algoritmen överraskande bra i många fall
- hanterar högdimensionella data väl. Lätt att parallellisera och hanterar stora data väl
- presterar bättre än mer komplicerade modeller när datauppsättningen är liten
svaghet
- den uppskattade sannolikheten är ofta felaktig på grund av det naiva antagandet., Inte idealisk för regressionsanvändning eller sannolikhetsuppskattning
- när data är rikliga tenderar andra mer komplicerade modeller att överträffa naiva Bayes
sammanfattning
naiva Bayes använder den mest grundläggande sannolikhetskunskapen och gör ett naivt antagande om att alla funktioner är oberoende. Trots enkelheten (vissa kan säga förenkling) ger naiva Bayes en anständig prestanda i många applikationer.
nu förstår du hur naiva Bayes fungerar, det är dags att prova det i verkliga projekt!