introduktionsguide om linjär programmering för (aspirerande) Dataforskare

introduktion

optimering är livsstilen. Vi har alla ändliga resurser och tid och vi vill göra det mesta av dem. Från att använda din tid produktivt att lösa supply chain problem för ditt företag-allt använder optimering. Det är ett särskilt intressant och relevant ämne inom datavetenskap.,

det är också ett mycket intressant ämne – Det börjar med enkla problem, men det kan bli väldigt komplext. Att dela en chokladkaka mellan syskon är till exempel ett enkelt optimeringsproblem. Vi tänker inte i matematiska termer när vi löser det. Å andra sidan kan utarbetandet av lager-och lagerstrategi för en e-tailer vara mycket komplex. Miljontals SKUs med olika popularitet i olika regioner som ska levereras i bestämd tid och resurser – du ser vad jag menar!,

linjär programmering (LP) är ett av de enklaste sätten att utföra optimering. Det hjälper dig att lösa några mycket komplexa optimeringsproblem genom att göra några förenklande antaganden. Som analytiker är du skyldig att komma över applikationer och problem som ska lösas genom linjär programmering.

av någon anledning får LP inte så mycket uppmärksamhet som det förtjänar när man lär sig datavetenskap. Så jag tänkte låta mig göra rättvisa åt den här fantastiska tekniken. Jag bestämde mig för att skriva en artikel som förklarar linjär programmering på enkel engelska., Jag har hållit innehållet så enkelt som möjligt. Tanken är att komma igång och glada över linjär programmering.

Obs! Om du vill lära dig detta i ett kursformat har vi curerat den här fria kursen för dig-linjär programmering för Datavetenskapspersonal

Innehållstabell

1. Vad är linjär programmering?,
   • grundläggande terminologier
   • processen för att definiera ett LP-problem
2. lösa linjärt Program med grafisk metod
3. lösa linjärt Program med R
4. lösa linjärt Program med OpenSolver
5. Simplex metod
6. Northwest Corner metod och minst kostnad metod
7. tillämpningar av linjär programmering

Vad är linjär programmering?

nu, vad är linjär programmering? Linjär programmering är en enkel teknik där vi skildrar komplexa relationer genom linjära funktioner och sedan hitta de optimala punkterna., Det viktiga ordet i föregående mening är avbildat. De verkliga relationerna kan vara mycket mer komplexa – men vi kan förenkla dem till linjära relationer.

program för linjär programmering finns överallt omkring dig. Du använder linjär programmering på personliga och professionella fronter. Du använder linjär programmering när du kör hemifrån till jobbet och vill ta den kortaste vägen. Eller när du har en projektleverans gör du strategier för att göra ditt lagarbete effektivt för leverans i tid.,

exempel på ett linjärt programmeringsproblem

låt oss säga att en FedEx-leveransman har 6 paket att leverera på en dag. Lageret ligger vid punkt A. De 6 leveransdestinationerna ges av U, V, W, X, Y och Z. siffrorna på linjerna anger avståndet mellan städerna. För att spara på bränsle och tid leverans personen vill ta den kortaste vägen.

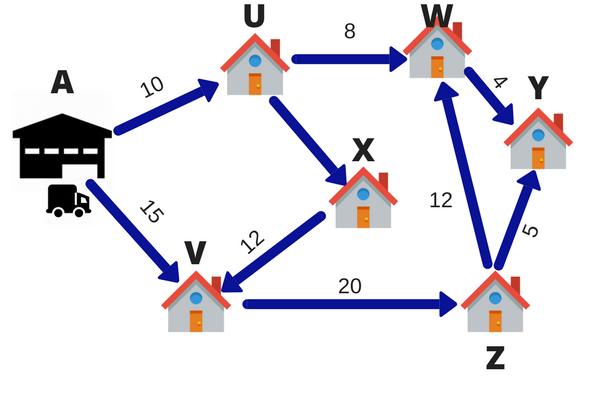
så kommer leveranspersonen att beräkna olika vägar för att gå till alla 6 destinationer och sedan komma med den kortaste vägen., Denna teknik för att välja den kortaste vägen kallas linjär programmering.

I detta fall är målet för leveranspersonen att leverera paketet i tid vid alla 6 destinationer. Processen att välja den bästa vägen kallas operationsforskning. Operationsforskning är ett tillvägagångssätt för beslutsfattande, vilket innebär en uppsättning metoder för att driva ett system. I ovanstående exempel var mitt system leveransmodellen.

linjär programmering används för att få den mest optimala lösningen för ett problem med givna begränsningar., I linjär programmering formulerar vi vårt verkliga problem till en matematisk modell. Det handlar om en objektiv funktion, linjära ojämlikheter med förbehåll för begränsningar.

är den linjära representationen av de 6 punkterna ovan representativa för den verkliga världen? Ja och nej. Det är en förenkling eftersom den verkliga vägen inte skulle vara en rak linje. Det skulle sannolikt ha flera varv, U-varv, signaler och trafikstockningar. Men med ett enkelt antagande har vi minskat problemets komplexitet drastiskt och skapar en lösning som borde fungera i de flesta scenarier.,

formulera ett problem – låt oss tillverka lite choklad

exempel: överväga ett chokladtillverkningsföretag som producerar endast två typer av choklad – A och B. både choklad kräver endast mjölk och Choco. För att tillverka varje enhet av A och B krävs följande kvantiteter:

• varje enhet av a kräver 1 enhet mjölk och 3 enheter Choco
• varje enhet av B kräver 1 enhet mjölk och 2 enheter Choco

företagets kök har totalt 5 enheter mjölk och 12 enheter Choco., På varje försäljning gör företaget en vinst på

• Rs 6 per enhet A såld
• Rs 5 per enhet B såld.

nu vill företaget maximera sin vinst. Hur många enheter av A och B ska det producera respektive?

lösning: det första jag ska göra är att representera problemet i en tabellform för bättre förståelse.,>

Rs 5 Total 5 12

låt det totala antalet enheter som produceras av en be = x

låt det totala antalet enheter som produceras av B be = y

nu representeras den totala vinsten av z

den totala vinsten som företaget gör ges av det totala antalet enheter av A och B som produceras multiplicerat med per enhet resultatet av RS 6 respektive RS 5.,

vinst: Max Z = 6X+5y

vilket innebär att vi måste maximera Z.

företaget kommer att försöka producera så många enheter av A och B för att maximera vinsten. Men resurserna mjölk och Choco finns i en begränsad mängd.

enligt ovanstående tabell kräver varje enhet av A och B 1 mjölkenhet. Den totala mängden mjölk som finns tillgänglig är 5 enheter., För att representera detta matematiskt,

X+Y ≤ 5

dessutom kräver varje enhet av A och B 3 enheter& 2 enheter Choco respektive. Den totala mängden Choco tillgänglig är 12 enheter. För att representera detta matematiskt,

3X+2y ≤ 12

även värdena för enheter av A kan endast vara heltal.,

så vi har ytterligare två begränsningar, X ≥ 0 & y ≥ 0

för att företaget ska kunna göra maximal vinst måste ovanstående ojämlikheter uppfyllas.

detta kallas att formulera ett verkligt problem till en matematisk modell.

vanliga terminologier som används i linjär programmering

låt oss definiera vissa terminologier som används i linjär programmering med hjälp av ovanstående exempel.

• Beslutsvariabler: beslutsvariablerna är de variabler som bestämmer min produktion., De representerar min ultimata lösning. För att lösa alla problem måste vi först identifiera beslutsvariablerna. För ovanstående exempel är det totala antalet enheter för A och B betecknade med X & Y respektive mina beslutsvariabler.
• objektiv funktion: det definieras som målet att fatta beslut. I ovanstående exempel vill företaget öka den totala vinsten som representeras av Z. Så vinst är min objektiva funktion.,
• begränsningar: begränsningarna är begränsningarna eller begränsningarna för beslutsvariablerna. De begränsar vanligtvis värdet av beslutsvariablerna. I ovanstående exempel är gränsen för tillgången på resurser mjölk och Choco mina begränsningar.
• icke-negativitetsbegränsning: för alla linjära program ska beslutsvariablerna alltid ta icke-negativa värden. Detta innebär att värdena för beslutsvariabler bör vara större än eller lika med 0.,

processen för att formulera ett linjärt programmeringsproblem

låt oss titta på stegen för att definiera ett linjärt programmeringsproblem generellt:

1. identifiera beslutsvariablerna
2. skriv målfunktionen
3. nämna begränsningarna
4. ange uttryckligen den icke-negativitetsbegränsningen

för att ett problem ska vara en linjär programmeringsproblem roblem, beslutsvariablerna, objektiv funktion och begränsningar måste alla vara linjära funktioner.,

om alla tre villkoren är uppfyllda kallas det ett linjärt programmeringsproblem.

Lös linjära program med grafisk metod

ett linjärt program kan lösas med flera metoder. I det här avsnittet kommer vi att titta på den grafiska metoden för att lösa ett linjärt program. Denna metod används för att lösa ett tvåvariabelt linjärt program. Om du bara har två beslutsvariabler ska du använda den grafiska metoden för att hitta den optimala lösningen.,

en grafisk metod innebär att man formulerar en uppsättning linjära ojämlikheter som är föremål för begränsningarna. Då ritas ojämlikheterna på ett X-Y-plan. När vi har ritat alla ojämlikheter på en graf ger den korsande regionen oss en genomförbar region. Den genomförbara regionen förklarar vad alla värderingar vår modell kan ta. Och det ger oss också den optimala lösningen.

låt oss förstå detta med hjälp av ett exempel.

exempel: en jordbrukare har nyligen förvärvat en 110 hektar mark., Han har bestämt sig för att odla vete och korn på det landet. På grund av solens kvalitet och regionens utmärkta klimat kan hela produktionen av vete och korn säljas.,h variation i 110 hektar, med tanke på kostnaderna, nettovinster och arbetskraven enligt de uppgifter som visas nedan:

sort	kostnad (pris/Hec)	nettovinst (pris/Hec)	man-dagar/Hec
vete	/td>	100	50	10
korn	200	120	30

bonden har en budget på 2 miljoner euro.av US$10,000 och tillgänglighet av 1,200 man-dagar under planeringshorisonten., Hitta den optimala lösningen och det optimala värdet.

lösning: för att lösa detta problem ska vi först formulera vårt linjära program.

formulering av linjärt Problem

Steg 1: Identifiera beslutsvariablerna

den totala arealen för odling av vete = X (i hektar)

den totala arealen för odling av korn = Y (i hektar)

X och Y är mina beslutsvariabler.

steg 2: Skriv målfunktionen

eftersom produktionen från hela marken kan säljas på marknaden. Bonden skulle vilja maximera vinsten för sin totala produktion., Vi får nettovinst för både vete och korn. Bonden tjänar en nettovinst på US $ 50 för varje hektar vete och us $ 120 för varje korn.

vår målfunktion (ges av Z) är, Max Z = 50X + 120Y

steg 3: skriva begränsningarna

1. Det är givet att bonden har en total budget på US $ 10,000. Kostnaden för att producera vete och korn per hektar ges också till oss. Vi har ett övre tak för den totala kostnaden för jordbrukaren. Så vår ekvation blir:

100X + 200Y ≤ 10,000

2., Nästa begränsning är det övre locket på tillgängligheten av det totala antalet mandagar för planeringshorisonten. Det totala antalet mandagar är 1200. Enligt tabellen får vi mandagarna per hektar för vete och korn.

10X + 30Y ≤ 1200

3. Den tredje begränsningen är den totala arealen som finns för plantage. Den totala tillgängliga arealen är 110 hektar., Så blir ekvationen,

X + Y ≤ 110

steg 4: icke-negativitetsbegränsningen

värdena för X och Y kommer att vara större än eller lika med 0. Detta är självklart.

x ≥ 0, Y ≥ 0

Vi har formulerat vårt linjära program. Det är dags att lösa det.

lösa en LP genom grafisk metod

eftersom vi vet att X, Y ≥ 0. Vi kommer bara att överväga den första kvadranten.

för att rita för grafen för ovanstående ekvationer, först kommer jag att förenkla alla ekvationer.,

100X + 200Y ≤ 10 000 kan förenklas till X + 2y ≤ 100 genom att dividera med 100.

10X + 30Y ≤ 1200 kan förenklas till X + 3Y ≤ 120 genom att dividera med 10.

den tredje ekvationen är i förenklad form, X + Y ≤ 110.

Rita de första 2 raderna på en graf i den första kvadranten (som visas nedan)

den optimala möjliga lösningen uppnås vid skärningspunkten där budgeten & begränsningar för mandagar är aktiva., Detta innebär den punkt där ekvationerna X + 2y ≤ 100 och X + 3y ≤ 120 skär ger oss den optimala lösningen.

värdena för X och Y som ger den optimala lösningen är vid (60,20).

för att maximera vinsten bör jordbrukaren producera vete och korn i 60 hektar respektive 20 hektar mark.,

den maximala vinsten som företaget kommer att få är,

Max Z = 50 * (60) + 120 * (20)

= us$5400

notera: allt som lärs här har också undervisats i ett kursformat i denna fria kurs – linjär programmering för datavetenskap proffs

lösa linjärt Program med R

R är en öppen källkod verktyg som är mycket populär bland Dataforskare för viktiga datavetenskap uppgifter. Att utföra linjär programmering är mycket lätt och vi kan uppnå en optimal lösning i mycket få steg. Kom, så lär vi oss.,

exempel: en leksakstillverkningsorganisation tillverkar två typer av leksaker A och B. Båda leksakerna säljs på Rs.25 och Rs.20 respektive. Det finns 2000 resursenheter tillgängliga varje dag från vilken leksaken a kräver 20 enheter medan toy B kräver 12 enheter. Båda dessa leksaker kräver en produktionstid på 5 minuter. Total arbetstid är 9 timmar om dagen. Vad ska vara tillverkningsmängden för var och en av rören för att maximera vinsten?

Här:

målfunktionen är:
Max.,Z=25x+20y

var X är enheterna för rör a

y är enheterna för rör b

Begränsningar:
20x+12y<=2000

5x+5y<=540

låt oss se koddelen nu:

utgång

därför från utgången ser vi att organisationen ska producera 88 enheter leksak a och 20 enheter leksak B och den maximala vinsten för organisationen kommer att vara rs.2600.,

Lös linjärt Program med OpenSolver

I verkligheten kan ett linjärt program innehålla 30 till 1000 variabler och lösa det antingen grafiskt eller algebraiskt är nästan omöjligt. Företag använder i allmänhet OpenSolver för att ta itu med dessa verkliga problem. Här ska jag ta dig genom steg för att lösa ett linjärt program med OpenSolver.

OpenSolver är en öppen källkod linjär och optimizer för Microsoft Excel. Det är en avancerad version av en inbyggd Excel-lösare. Du kan ladda ner OpenSolver här och följa installationsmanualen.,

Jag vill att du ska få praktisk kunskap om att använda OpenSolver. Så, för en klar förståelse, kommer jag att förklara det med ett exempel.

exempel: nedan finns ett dietdiagram som ger mig kalorier, protein, kolhydrater och fettinnehåll för 4 matvaror. Sara vill ha en diet med minimal kostnad., The diet chart is as follows:

	Food Item 1	Food Item 2	Food Item 3	Food Item 4
Calories	400	200	150	500
Protien (in grams)	3	2	0	0
Carbohydrates ( in grams)	2	2	4	4
Fat (in grams)	2	4	1	5
Cost	$0.50	$0.20	$0.,30	$0.80

diagrammet ger näringsinnehållet samt kostnaden per enhet för varje livsmedelsartikel. Dieten måste planeras på ett sådant sätt att det ska innehålla minst 500 kalorier, 6 gram protein, 10 gram kolhydrater och 8 gram fett.

lösning: först ska jag formulera mitt linjära program i ett kalkylblad.

• Steg 1: Identifiera beslutsvariablerna. Här är mina beslutsvariabler matvarorna. Lägg till rubrikerna., För försöksändamål går vi in i godtyckliga värden. Låt oss säga, Sara förbrukar 3 enheter livsmedel objekt 1, 0 enhet livsmedel objekt 2, 1 enhet livsmedel objekt 3 och 0 enhet livsmedel objekt 4. Dessa kallas variabla celler.

• steg 2: Nu skriver vi vår objektiva funktion. För att kosten ska vara optimal måste vi ha minimal kostnad tillsammans med nödvändiga kalorier, protein, kolhydrater och fett.

I cell B7:E7 tar vi hänvisningen till antalet enheter., Och i cell B8: E8 sätter vi kostnaden per enhet för varje livsmedelsartikel.

I cell B10 vill vi ha den totala kostnaden för kosten. Den totala kostnaden ges av sumpprodukten av antalet enheter som ätas och per enhetskostnad. Produktsumma ges av = B7*B8+C7*C8+D7*D8+E7*E8. Låt oss se detta i ett kalkylblad.

• steg 3: nu kommer vi att ange begränsningarna. Kolumn F innehåller totalt kalorier, protein, kolhydrater och fett., Det totala antalet kaloriintag i givet av sumproduct antalet matvaror som ätas och kalori konsumeras per matvara. För cell F13= Sumprodcut($B$7:$F$7, B13:F13). På samma sätt för andra. Kolumn G ger ojämlikheten eftersom problemet kräver att kalorier, Protein, kolhydrater och fett ska vara minst 500, 6, 10 respektive 8. Kolumn H ger det näringsinnehåll som krävs.

• steg 4: Nu kommer vi in i det linjära programmet i lösare. Nu, när du har installerat OpenSolver., När du klickar på fliken Data, till höger ser du modellen. Klicka på modellen och ange sedan värdena en efter en. Först kommer vi in i målfunktionen,$B10 dvs i målcellen. Välj minimera eftersom vi vill minimera kostkostnaden.

• Steg 5: Ange nu beslutsvariablerna i variabelcellerna.

• steg 6: Nu lägger vi till begränsningarna. Den första begränsningen är F13 ≥ H13. Lägg till alla begränsningar en efter en.,

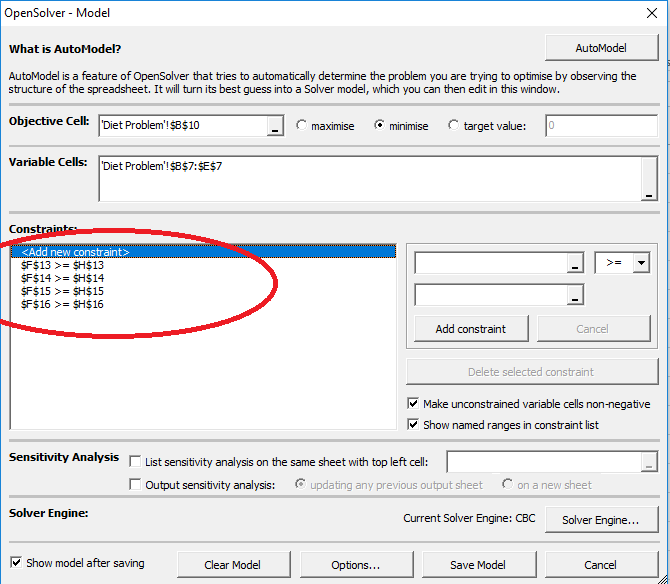
• Steg 7: Nu måste du ange en viktig begränsning. Den icke-negativitetsbegränsningen. Alla beslutsvariabler kommer att vara större än 0.

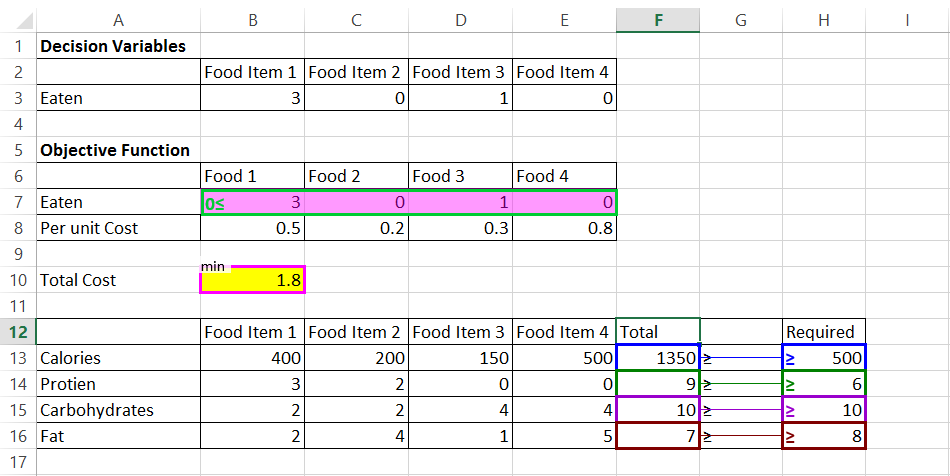
• steg 8: Klicka nu på Spara modell för att avsluta modelleringsprocessen. När du sparar modellen kommer det att se ut så här.

• steg 9: när modellen har sparats klickar du på fliken Data och klickar sedan på lös., Den optimala lösningen och värdena visas i motsvarande celler. Den optimala minimikostnaden är us $ 0.90. Sara bör konsumera 3 enheter av livsmedel objekt 2 och 1 enhet av livsmedel objekt 3 för den nödvändiga näringsinnehåll till lägsta kostnad. Detta löser vårt linjära program.

Simplex metod

Simplex metod är en av de mest kraftfulla & populära metoder för linjär programmering. Simplexmetoden är ett iterativt förfarande för att få den mest genomförbara lösningen., I den här metoden fortsätter vi att omvandla värdet av grundläggande variabler för att få maximalt värde för målfunktionen.

en linjär programmeringsfunktion är i sin standardform om den försöker maximera målfunktionen. med förbehåll för begränsningar,

. . . . . .

. . . . . .

var, och., Efter att ha lagt till slackvariabler är motsvarande system för begränsningsekvation,

. . . .

var,

variablerna, ………………. kallas slack variabler. De är icke-negativa tal som läggs till för att ta bort ojämlikheterna från en ekvation.

ovanstående förklaring ger den teoretiska förklaringen av simplexmetoden., Nu ska jag förklara hur man använder simplexmetoden i verkliga livet med Excel.

exempel: annonsalternativen för ett företag inkluderar TV, tidningar och radioannonser. Kostnaden för varje medium med sin publik täckning ges nedan.,

	Television	Newspaper	Radio
Cost per advertisement ($)	2000	600	300
Audience per advertisement	100,000	40,000	18,000

The local newspaper limits the number of advertisements from a single company to ten., För att balansera annonseringen bland de tre typerna av media bör inte mer än hälften av det totala antalet annonser förekomma på radion. Och minst 10% bör förekomma på TV. Veckans reklambudget är $ 18,200. Hur många annonser ska köras i var och en av de tre typerna av media för att maximera den totala publiken?

lösning: först ska jag formulera mitt problem för en klar förståelse.,

Steg 1: Identifiera Beslutsvariabler

låt,, representera det totala antalet annonser för TV, tidning respektive radio.

steg 2: objektiv funktion

syftet med företaget är att maximera publiken. Målfunktionen ges av:

steg 3: Skriv ner begränsningarna

nu kommer jag att nämna varje begränsning en efter en.

det är tydligt att vi har en budgetbegränsning., Den totala budgeten som kan tilldelas är $ 18,200. Och de individuella kostnaderna per tv, tidning och radio annons är $2000, $600 och $300 respektive. Detta kan representeras av ekvationen,

för en tidningsannons finns det ett övre lock på antalet annonser till 10. Mina första begränsningar är,

nästa begränsning är antalet annonser på TV., Företaget vill att minst 10% av de totala annonserna ska vara på TV. Så det kan representeras som:

den sista begränsningen är att antalet annonser på radion inte kan vara mer än hälften av det totala antalet annonser. Det kan representeras som

nu har jag formulerat mitt linjära programmeringsproblem. Vi använder simplex-metoden för att lösa detta. Jag tar dig genom simplexmetoden en efter en.

för att upprepa alla begränsningar är följande., I have simplified the last two equations to bring them in standard form.

We have a total of 4 equations. To balance out each equation, I am introducing 4 slack variables, , and .,

så våra ekvationer är följande:

jag hoppas nu att du är tillgänglig för att förstå hela annonseringsproblemet. Alla ovanstående ekvationer är bara för din bättre förståelse. Nu om du löser dessa ekvationer får du värdena för X1= 4, X2= 10 och X3 = 14.

om du löser målfunktionen får du den maximala veckovisa publiken som 1,052,000., Du kan följa handledningen här för att lösa ekvationen. För att lösa ett linjärt program i excel, följ den här handledningen.

Northwest Corner Method and Least Cost Method

6.1 Northwest Corner Method

northwest corner method är en speciell typmetod som används för transportproblem vid linjär programmering. Det används för att beräkna den genomförbara lösningen för transport av varor från en plats till en annan. När du får ett verkligt problem, vilket innebär tillgång och efterfrågan från en källa till olika källor., Datamodellen innehåller följande:

• nivån på utbud och efterfrågan vid varje källa ges
• enhetstransporten av en vara från varje källa till varje destination

modellen förutsätter att det bara finns en vara. Efterfrågan som kan komma från olika källor. Målet är att uppfylla den totala efterfrågan med minsta transportkostnad. Modellen bygger på hypotesen att den totala efterfrågan är lika med det totala utbudet, dvs. modellen är balanserad. Låt oss förstå detta med hjälp av ett exempel.,

exempel: Tänk på att det finns 3 silor som krävs för att tillgodose efterfrågan från 4 kvarnar. (En silo är en lagringsplats för den gård som används för att lagra spannmål och kvarn är en slipfabrik för korn).

lösning: Låt oss förstå vad ovanstående tabell förklarar.

kostnaden för transport från Silo i till Mill j ges av kostnaden i varje cell som motsvarar utbudet från varje silo 1 och efterfrågan vid varje Kvarn., Till exempel är kostnaden för transport från Silo 1 till Mill 1 $ 10, från Silo 3 till Mill 5 är $ 18. Det ges också den totala efterfrågan & leverans för kvarn och silor. Målet är att hitta den minimala transportkostnaden så att efterfrågan på alla fabriker är nöjd.

eftersom namnet antyder Northwest corner method är en metod för att allokera enheterna från den övre vänstra cellen. Efterfrågan på Mill 1 är 5 och Silo 1 har ett totalt utbud av 15. Så, 5 enheter kan tilldelas Mill1 till en kostnad av $ 10 per enhet. Efterfrågan på Mill1 är uppfylld., sedan flyttar vi till den övre vänstra cellen i Mill 2. Efterfrågan på Mill 2 är 15 enheter, som det kan få 10 enheter från Silo 1 till en kostnad av $2 per enhet och 5 enheter från Silo 2 till en kostnad av $7 per enhet. Sedan går vi vidare till Mill 3, den nordvästra cellen är s2m3. Efterfrågan på Bruket 3 är 15 enheter, som det kan bli från Silo 2 till en kostnad av $9 per enhet. Går vidare till den sista kvarnen, Mill 4 har en efterfrågan på 15 enheter. Det kommer att få 5 enheter från en Silo 2 till en kostnad av $ 20 per enhet och 10 enheter från Silo 3 till en kostnad av $ 18 per enhet.,

den totala kostnaden för transport är = 5*10+(2*10+7*5)+9*15+(20*5+18*10) = $520

6.2 minsta kostnadsmetod

minst kostnadsmetod är en annan metod för att beräkna den mest genomförbara lösningen för ett linjärt programmeringsproblem. Denna metod ger mer exakta resultat än Northwest corner-metoden. Den används för transport och tillverkningsproblem. För att hålla det enkelt förklarar jag ovanstående transportproblem.,

enligt den lägsta kostnadsmetoden börjar du från cellen som innehåller minst enhetskostnad för transport. Så, för ovanstående problem, levererar jag 5 enheter från Silo 3 till en per enhetskostnad på $4. Efterfrågan på Mill1 är uppfylld. För Mill 2 levererar vi 15 enheter från Silo 1 till en per enhetskostnad på $2. Sedan för Mill 3 levererar vi 15 enheter från Silo 2 till en per enhetskostnad på $ 9. Sedan för Mill 4 levererar vi 10 enheter från Silo 2 till en per enhetskostnad på $ 20 och 5 enheter från Silo 3 en $18 per enhet., De totala transportkostnaderna är $ 475.

Tja, ovanstående metod förklarar att vi kan optimera våra kostnader ytterligare med den bästa metoden. Låt oss kolla detta med Excel Solver. Solver är ett inbyggt tillägg i Microsoft Excel. Det är en tilläggsplugg som finns i Excel. Gå till fil->alternativ->tillägg->välj lösare->klicka på Hantera->välj lösare->klicka på OK. Din lösare läggs nu till i excel. Du kan kontrollera det under fliken Data.,

det första jag ska göra är att ange mina data i excel. Efter att ha skrivit in data i excel har jag beräknat summan av C3: F3. På samma sätt för andra. Detta görs för att ta den totala efterfrågan från Silo 1 och andra.

efter detta kommer jag att bryta min modell i två. Den första tabellen ger mig de levererade enheterna och den andra tabellen ger mig enhetskostnaden.,

nu beräknar jag min totala kostnad som kommer att ges av Sumproduct av enhetskostnad och levererade enheter.

nu ska jag använda Solver för att beräkna min modell. Liknar ovanstående metod. Lägg till målfunktionen, variabla celler, begränsningar.

nu är din modell redo att lösas. Klicka på lös och du får din optimala kostnad., Minsta transportkostnaden är $435.

tillämpningar av linjär programmering

linjär programmering och optimering används i olika branscher. Tillverknings-och serviceindustrin använder regelbundet linjär programmering. I det här avsnittet kommer vi att titta på de olika tillämpningarna av linjär programmering.

1. tillverkningsindustrier använder linjär programmering för att analysera deras försörjningskedjeverksamhet. Deras motiv är att maximera effektiviteten med minsta driftskostnad., Enligt rekommendationerna från den linjära programmeringsmodellen kan tillverkaren omkonfigurera sin lagringslayout, justera sin arbetskraft och minska flaskhalsarna. Här är en liten lager fallstudie av Cequent ett USA-baserat företag, titta på den här videon för en tydligare förståelse.
2. linjär programmering används också i organiserad detaljhandel för hyllutrymme optimering. Eftersom antalet produkter på marknaden har ökat med stormsteg är det viktigt att förstå vad kunden vill ha., Optimering används aggressivt i butiker som Walmart, Hypercity, Reliance, Big Bazaar, etc. Produkterna i butiken placeras strategiskt med tanke på kund shoppingmönstret. Målet är att göra det enkelt för en kund att hitta & Välj rätt produkter. Detta är föremål för begränsningar som begränsad hylla utrymme, en mängd olika produkter, etc.
3. optimering används också för att optimera leveransvägar. Detta är en förlängning av det populära resande säljare problemet., Servicebranschen använder optimering för att hitta den bästa vägen för flera säljare som reser till flera städer. Med hjälp av klustring och girig algoritm bestäms leveransrutterna av företag som FedEx, Amazon etc. Målet är att minimera driftskostnaden och tiden.
4. optimeringar används också i maskininlärning. Övervakat lärande fungerar på grund av linjär programmering. Ett system är utbildad för att passa på en matematisk modell av en funktion från de märkta indata som kan förutsäga värden från en okänd testdata.,

Tja, applikationerna för linjär programmering slutar inte här. Det finns många fler tillämpningar av linjär programmering i verkliga världen som tillämpas av aktieägare, Sport, aktiemarknader, etc. Gå vidare och utforska vidare.

slutnot

jag hoppas att du tyckte om att läsa den här artikeln. Jag har försökt förklara alla grundläggande begrepp under linjär programmering. Om du har några tvivel eller frågor Är du välkommen att skicka dem i kommentarfältet., För enkel förståelse har vi brutit den här långa artikeln i ett kortare kursformat-linjär programmering för Datavetenskapspersonal

jag har förklarat varje koncept med ett verkligt exempel. Jag vill att du försöker med dem och får praktisk erfarenhet. Låt mig veta vad du tycker!

lär dig, tävla, hacka och bli anställd!

du kan också läsa den här artikeln i vår mobilapp