Introduction guide on Linear Programming for (aspiring)data scientists

Introduction

Optimization is the way of life. We hebben allemaal eindige middelen en tijd en we willen er het beste van maken. Van uw tijd productief gebruiken tot het oplossen van supply chain problemen voor uw bedrijf – alles maakt gebruik van optimalisatie. Het is een bijzonder interessant en relevant onderwerp in data science.,

Het is ook een zeer interessant onderwerp – het begint met eenvoudige problemen, maar het kan zeer complex worden. Bijvoorbeeld, het delen van een reep chocolade tussen broers en zussen is een eenvoudig optimalisatie probleem. We denken niet in wiskundige termen terwijl we het oplossen. Aan de andere kant kan het opstellen van een voorraad-en warehousingstrategie voor een e-tailer erg complex zijn. Miljoenen SKU ’s met verschillende populariteit in verschillende regio’ s worden geleverd in gedefinieerde tijd en middelen – u begrijpt wat ik bedoel!,

lineair programmeren (LP) is een van de eenvoudigste manieren om optimalisatie uit te voeren. Het helpt u een aantal zeer complexe optimalisatie problemen op te lossen door het maken van een paar vereenvoudiging aannames. Als analist kom je vast en zeker applicaties en problemen tegen die opgelost moeten worden door lineair te programmeren.

om de een of andere reden krijgt LP niet zoveel aandacht als het verdient tijdens het leren van data science. Dus, ik dacht laat me recht doen aan deze geweldige techniek. Ik besloot een artikel te schrijven dat lineair programmeren in eenvoudig Engels uitlegt., Ik heb de inhoud zo eenvoudig mogelijk gehouden. Het idee is om je op weg te helpen en enthousiast te worden over lineair programmeren.

Opmerking-Als u dit in een cursus formaat wilt leren, hebben we deze gratis cursus voor u samengesteld-lineair programmeren voor Data Science Professionals

inhoudsopgave

1. Wat is lineair programmeren?,
   • Basisterminologieën
   • het proces om een LP-probleem te definiëren
2. lineair programma oplossen met behulp van een grafische methode
3. lineair programma oplossen met behulp van R
4. lineair programma oplossen met behulp van OpenSolver
5. Simplex methode
6. Northwest Corner methode en Least Cost methode
7. toepassingen van lineair programmeren

Wat is lineair programmeren?

nu, wat is lineair programmeren? Lineair programmeren is een eenvoudige techniek waarbij we complexe relaties via lineaire functies afbeelden en vervolgens de optimale punten vinden., Het belangrijke woord in de vorige zin is afgebeeld. De echte relaties zijn misschien veel complexer – maar we kunnen ze vereenvoudigen tot lineaire relaties.

toepassingen van lineair programmeren zijn overal om je heen. Je gebruikt lineair programmeren op persoonlijke en professionele fronten. U gebruikt lineaire programmering wanneer u van huis naar werk rijdt en de kortste route wilt nemen. Of wanneer u een project levering u strategieën om uw team efficiënt te laten werken voor tijdige levering.,

voorbeeld van een lineair programmeerprobleem

laten we zeggen dat een FEDEX bezorger 6 pakketten heeft om op een dag te leveren. Het magazijn bevindt zich op punt A. de 6 afleverbestemmingen worden gegeven door U, V, W, X, Y en Z. De nummers op de lijnen geven de afstand tussen de steden aan. Om brandstof en tijd te besparen wil de bezorger de kortste route nemen.

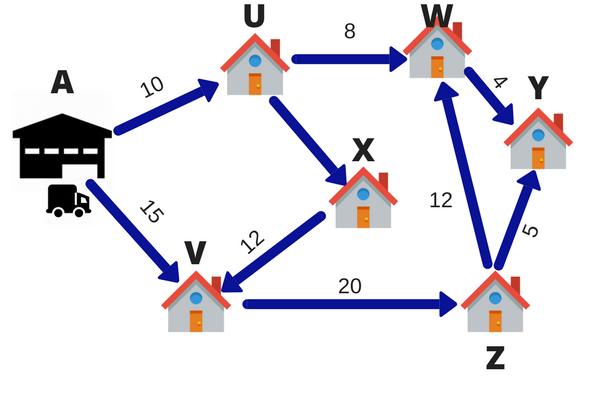
de bezorger berekent dus verschillende routes om naar alle 6 bestemmingen te gaan en komt dan met de kortste route., Deze techniek om de kortste route te kiezen wordt lineair programmeren genoemd.

in dit geval is het doel van de bezorger om het pakket op tijd te leveren op alle 6 bestemmingen. Het proces van het kiezen van de beste route heet Operation Research. Operation research is een benadering van besluitvorming, waarbij een reeks methoden om een systeem te bedienen. In het bovenstaande voorbeeld, mijn systeem was de levering model.

lineaire programmering wordt gebruikt voor het verkrijgen van de meest optimale oplossing voor een probleem met bepaalde beperkingen., In lineair programmeren formuleren we ons echte probleem in een wiskundig model. Het gaat om een objectieve functie, lineaire ongelijkheden met beperkingen.

is de lineaire weergave van de 6 punten hierboven representatief voor de reële wereld? Ja En Nee. Het is een oversimplificatie omdat de echte route geen rechte lijn zou zijn. Het zou waarschijnlijk meerdere bochten, U-bochten, signalen en files. Maar met een simpele aanname hebben we de complexiteit van het probleem drastisch verminderd en creëren we een oplossing die in de meeste scenario ‘ s zou moeten werken.,

het formuleren van een probleem – laten we enkele chocolade maken

voorbeeld: beschouw een chocoladefabrikant die slechts twee soorten chocolade produceert – A en B. Beide chocolade vereist alleen melk en Choco. Voor de vervaardiging van elke eenheid van A en B zijn de volgende hoeveelheden vereist:

• elke eenheid van A vereist 1 eenheid melk en 3 eenheden Choco
• elke eenheid van B vereist 1 eenheid melk en 2 eenheden Choco

de bedrijfskeuken heeft in totaal 5 eenheden melk en 12 eenheden Choco., Bij elke verkoop maakt de onderneming een winst van

• Rs 6 per verkochte eenheid a
• Rs 5 per verkochte eenheid B.

nu wil het bedrijf zijn winst maximaliseren. Hoeveel eenheden van A en B moet het respectievelijk produceren?

oplossing: het eerste wat ik ga doen is het probleem in een tabelvorm weergeven voor een beter begrip.,>

Rs 5 Totaal 5 12

Laten we het totale aantal eenheden geproduceerd door A = X

Laten we het totale aantal eenheden geproduceerd door B = Y

Nu, de totale winst wordt vertegenwoordigd door Z

De totale winst die het bedrijf maakt wordt bepaald door het totale aantal eenheden van A en B geproduceerd, vermenigvuldigd met het per-eenheid winst van Rs 6 en Rs 5 respectievelijk.,

winst: Max Z = 6X+5Y

wat betekent dat we Z.

moeten maximaliseren om de winst te maximaliseren. Maar de middelen melk en Choco zijn beschikbaar in een beperkte hoeveelheid.

volgens bovenstaande tabel vereist elke eenheid van A en B 1 eenheid melk. De totale hoeveelheid melk die beschikbaar is is 5 eenheden., Om dit wiskundig weer te geven,

X+Y ≤ 5

ook vereist elke eenheid van A en B 3 eenheden & 2 eenheden van respectievelijk Choco. De totale hoeveelheid Choco beschikbaar is 12 eenheden. Om dit wiskundig weer te geven, kunnen

3X+2y ≤ 12

ook kunnen de waarden voor eenheden van A alleen gehele getallen zijn.,

dus we hebben nog twee beperkingen, X ≥ 0 & Y ≥ 0

om maximale winst te maken, moet aan de bovenstaande ongelijkheden worden voldaan.

Dit wordt het formuleren van een reëel probleem in een wiskundig model genoemd.

gemeenschappelijke terminologieën gebruikt in lineaire programmering

laten we enkele terminologieën gebruikt in lineaire programmering definiëren met behulp van het bovenstaande voorbeeld.

• Beslissingsvariabelen: de beslissingsvariabelen zijn de variabelen die mijn uitvoer bepalen., Ze vertegenwoordigen mijn ultieme oplossing. Om een probleem op te lossen, moeten we eerst de beslissingsvariabelen identificeren. In het bovenstaande voorbeeld is het totale aantal eenheden voor A en B aangeduid met X & Y respectievelijk mijn beslissingsvariabelen.
• objectieve functie: het wordt gedefinieerd als het doel van het nemen van beslissingen. In het bovenstaande voorbeeld wil het bedrijf de totale winst, vertegenwoordigd door Z. verhogen dus, winst is mijn objectieve functie.,
• beperkingen: de beperkingen zijn de beperkingen of beperkingen op de beslissingsvariabelen. Ze beperken meestal de waarde van de beslissingsvariabelen. In het bovenstaande voorbeeld, de limiet op de beschikbaarheid van middelen melk en Choco zijn mijn beperkingen.
• non-negativity restriction: voor alle lineaire programma ‘ s moeten de beslissingsvariabelen altijd niet-negatieve waarden aannemen. Dit betekent dat de waarden voor beslissingsvariabelen groter of gelijk moeten zijn aan 0.,

Het proces is het formuleren van een Lineaire Programmering probleem

Laten we eens kijken naar de stappen van het definiëren van een Lineaire Programmering probleem algemeen:

1. het Identificeren van de variabelen besluit
2. Schrijf de objectieve functie
3. Vermelding van de beperkingen
4. Expliciet vermeld dat de niet-negativiteit beperking

Voor een probleem te worden in een lineaire programmering probleem, de variabelen besluit, objectieve functie en beperkingen hebben lineaire functies.,

als aan alle drie de voorwaarden is voldaan, wordt dit een lineair Programmeerprobleem genoemd.

Lineaire programma ‘ s oplossen met grafische methode

een lineair programma kan met meerdere methoden worden opgelost. In deze sectie gaan we kijken naar de grafische methode voor het oplossen van een lineair programma. Deze methode wordt gebruikt om een twee-variabel lineair programma op te lossen. Als je slechts twee beslissingsvariabelen hebt, moet je de grafische methode gebruiken om de optimale oplossing te vinden.,

een grafische methode omvat het formuleren van een reeks lineaire ongelijkheden, afhankelijk van de beperkingen. Dan worden de ongelijkheden uitgezet op een X-Y vlak. Zodra we alle ongelijkheden op een grafiek hebben uitgezet, geeft het snijgebied ons een haalbaar gebied. De haalbare regio legt uit wat alle waarden van ons model zijn. En het geeft ons ook de optimale oplossing.

laten we dit begrijpen met behulp van een voorbeeld.

voorbeeld: een landbouwer heeft onlangs een stuk grond van 110 hectare verworven., Hij heeft besloten om tarwe en gerst te verbouwen op dat land. Door de kwaliteit van de zon en het uitstekende klimaat in de regio kan de gehele productie van tarwe en gerst worden verkocht.,h verscheidenheid in de 110 hectare, gezien de kosten, de netto winst en arbeid eisen volgens de gegevens hieronder getoond:

de Verschillende	Kosten (Prijs/Hec)	Netto Winst (Prijs/Hec)	Man-dagen/Hec
Tarwe	100	50	10
Gerst	200	120	30

De boer heeft een budget van US$10.000 en de beschikbaarheid van 1.200 man-dagen tijdens de planningshorizon., Vind de optimale oplossing en de optimale waarde.

oplossing: om dit probleem op te lossen, gaan we eerst ons lineaire programma formuleren.

formulering van Het lineaire probleem

Stap 1: Identificeer de beslissingsvariabelen

de totale oppervlakte voor de teelt van tarwe = X (in hectaren)

de totale oppervlakte voor de teelt van gerst = Y (in hectaren)

X en Y zijn mijn beslissingsvariabelen.

Stap 2: Schrijf de objectieve functie

omdat de productie van de gehele grond op de markt kan worden verkocht. De boer zou de winst voor zijn totale productie willen maximaliseren., We krijgen nettowinst voor zowel tarwe als gerst. De Boer verdient een nettowinst van US $ 50 per hectare tarwe en US $ 120 per gerst.

onze objectieve functie (gegeven door Z) is, Max Z = 50X + 120Y

Stap 3: schrijven van de beperkingen

1. Gezien het feit dat de Boer een totaal budget van US$10.000 heeft. De kosten voor de productie van tarwe en gerst per hectare worden ook aan ons gegeven. Wij hebben een bovengrens voor de totale kosten van de Boer. Dus onze vergelijking wordt:

100X + 200Y ≤ 10.000

2., De volgende beperking is de bovengrens voor de beschikbaarheid van het totale aantal mandagen voor de planningshorizon. Het totale aantal beschikbare mandagen bedraagt 1200. Volgens de tabel krijgen we de man-dagen per hectare voor tarwe en gerst.

10X + 30Y ≤ 1200

3. De derde beperking is de totale oppervlakte die aanwezig is voor de aanplanting. De totale beschikbare oppervlakte bedraagt 110 hectare., Dus de vergelijking wordt,

X + Y ≤ 110

Stap 4: de niet-negativiteits beperking

de waarden van X en Y zullen groter zijn dan of gelijk zijn aan 0. Dit spreekt voor zich.

X ≥ 0, Y ≥ 0

we hebben ons lineaire programma geformuleerd. Het is tijd om het op te lossen.

het oplossen van een LP door middel van grafische methode

omdat we weten dat X, Y ≥ 0. We beschouwen alleen het eerste kwadrant.

om de grafiek voor de bovenstaande vergelijkingen te plotten, zal ik eerst alle vergelijkingen vereenvoudigen.,

100X + 200Y ≤ 10.000 kan worden vereenvoudigd tot X + 2Y ≤ 100 door te delen door 100.

10X + 30Y ≤ 1200 kan worden vereenvoudigd tot X + 3Y ≤ 120 door te delen door 10.

de derde vergelijking is in vereenvoudigde vorm, X + Y ≤ 110.

teken de eerste 2 Regels op een grafiek in het eerste kwadrant (zoals hieronder weergegeven)

De optimale haalbare oplossing wordt bereikt op het snijpunt waar de begroting& man-dagenbeperkingen actief zijn., Dit betekent dat het punt waarop de vergelijkingen X + 2Y ≤ 100 en X + 3Y ≤ 120 elkaar snijden ons de optimale oplossing geeft.

de waarden voor X en Y, die de optimale oplossing geven, liggen op (60,20).

om de winst te maximaliseren moet de landbouwer tarwe en gerst produceren in respectievelijk 60 hectare en 20 hectare grond.,

De maximale winst van de vennootschap zal krijgen is,

Max Z = 50 * (60) + 120 * (20)

= US$5400

Opmerking: Alles geleerd heeft hier ook geleerd in een cursus in deze gratis cursus – Lineaire Programmering voor Data Science Professionals

het Oplossen van Lineaire Programma Met R

R is een open-source tool die erg populair is onder de gegevens wetenschappers voor essentiële data science taken. Lineair programmeren is heel eenvoudig en we kunnen in zeer weinig stappen een optimale oplossing bereiken. Kom, laten we het leren.,

voorbeeld: een speelgoedfabrikant produceert twee soorten speelgoed A en B. Beide speelgoed wordt verkocht aan Rs.25 en Rs.20 respectievelijk. Er zijn elke dag 2000 resource units beschikbaar waarvan de toy a 20 eenheden vereist, terwijl toy B 12 eenheden vereist. Beide speelgoed vereisen een productietijd van 5 minuten. De totale werkuren zijn 9 uur per dag. Wat moet de productie hoeveelheid voor elk van de buizen om de winst te maximaliseren?

Hier:

de objectieve functie is:
Max.,Z=25x+20y

x zijn de eenheden van de pijp Een

y zijn de eenheden van buis B

Beperkingen:
20x+12y<=2000

5x+5y<=540

Laten we eens kijken de code nu:

Output:

Daarom vanaf de uitgang, we zien dat de organisatie zou moeten produceren 88 eenheden van Een speeltje en 20 eenheden van speelgoed B en de maximale winst voor de organisatie Rs.2600.,

Los lineair programma op met behulp van OpenSolver

in werkelijkheid kan een lineair programma 30 tot 1000 variabelen bevatten en is het vrijwel onmogelijk om het Grafisch of algebraïsch op te lossen. Bedrijven gebruiken over het algemeen OpenSolver om deze reële problemen aan te pakken. Hier ga ik je door stappen nemen om een lineair programma op te lossen met behulp van OpenSolver.

OpenSolver is een open-source lineaire en optimizer voor Microsoft Excel. Het is een geavanceerde versie van een ingebouwde Excel Solver. U kunt OpenSolver hier downloaden en de installatiehandleiding volgen.,

Ik wil dat je praktische kennis krijgt over het gebruik van OpenSolver. Dus, voor een duidelijk begrip, zal ik het uitleggen aan de hand van een voorbeeld.

voorbeeld: hieronder is er een dieetkaart die me calorieën, eiwitten, koolhydraten en vetten geeft voor 4 voedingsmiddelen. Sara wil een dieet met minimale kosten., The diet chart is as follows:

	Food Item 1	Food Item 2	Food Item 3	Food Item 4
Calories	400	200	150	500
Protien (in grams)	3	2	0	0
Carbohydrates ( in grams)	2	2	4	4
Fat (in grams)	2	4	1	5
Cost	$0.50	$0.20	$0.,30	$0,80

de grafiek geeft het nutriëntengehalte en de kosten per eenheid van elk voedingsmiddel weer. Het dieet moet zo worden gepland dat het minstens 500 calorieën, 6 gram eiwit, 10 gram koolhydraten en 8 gram vet bevat.

oplossing: eerst formuleer ik mijn lineaire programma in een spreadsheet.

• stap 1: Identificeer de beslissingsvariabelen. Hier zijn mijn beslissingsvariabelen de voedselproducten. Voeg de headers toe., Voor proefdoeleinden voeren we willekeurige waarden in. Laten we zeggen, Sara verbruikt 3 eenheden van voedsel punt 1, 0 eenheid van voedsel punt 2, 1 eenheid van voedsel punt 3 en 0 eenheid van voedsel punt 4. Deze worden variabele cellen genoemd.

• stap 2: nu schrijven we onze objectieve functie. Om het dieet optimaal te laten zijn, moeten we minimale kosten hebben, samen met de benodigde calorieën, eiwitten, koolhydraten en vet.

in cel B7:E7 nemen we de verwijzing naar het aantal eenheden., En in cel B8: E8 zetten we de kosten per eenheid van elk voedselitem.

in cel B10 willen we de totale kosten van het dieet. De totale kosten worden gegeven door het SOMPRODUCT van het aantal eenheden gegeten en per eenheid kosten. SOMPRODUCT wordt gegeven door = B7 * B8+C7 * C8+D7*D8+E7 * E8. Laten we dit in een spreadsheet bekijken.

• stap 3: nu zullen we de beperkingen invoeren. Kolom F bevat in totaal calorieën, eiwitten, koolhydraten en vetten., Het totale aantal calorie-inname in gegeven door sumproduct het aantal voedsel items gegeten en de calorie geconsumeerd per voedsel item. Voor cel F13= Sumprodcut ($B $ 7:$F $ 7, B13: F13). Ook voor anderen. Kolom G geeft de ongelijkheid omdat het probleem vereist calorieën, eiwit, koolhydraten en vet ten minste 500, 6, 10 en 8 respectievelijk. Kolom H geeft het vereiste gehalte aan nutriënten aan.

• stap 4: Nu zullen we het lineaire programma in de oplosser invoeren. Nu, zodra u OpenSolver hebt geïnstalleerd., Wanneer u op het tabblad Gegevens klikt, ziet u rechts het Model. Klik op het model en voer de waarden één voor één in. Eerst zullen we de objectieve functie invoeren,$B10 dwz in de objectieve cel. Selecteer minimaliseren omdat we willen het dieet kosten te minimaliseren.

• Stap 5: Voer nu de beslissingsvariabelen in de variabele cellen in.

• Stap 6: nu zullen we de beperkingen toevoegen. De eerste beperking is de F13 ≥ H13. Voeg alle beperkingen één voor één toe.,

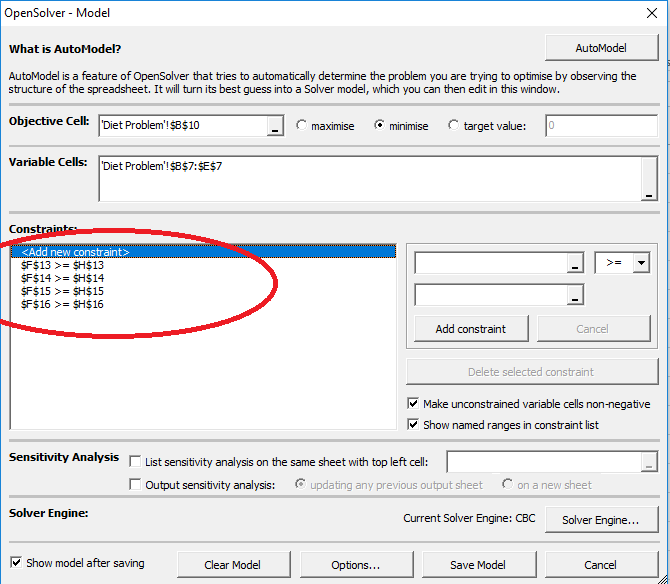
• stap 7: Nu moet u één belangrijke beperking invoeren. De niet-negativiteit beperking. Alle beslissingsvariabelen zullen groter zijn dan 0.

• stap 8: Klik nu op model Opslaan om het modelleringsproces te voltooien. Als je het model opslaat, ziet het er ongeveer zo uit.

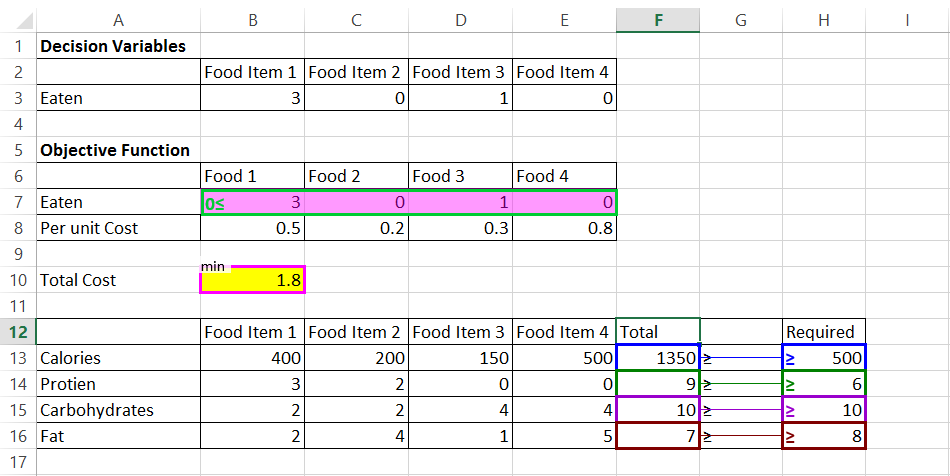
• stap 9: zodra het model is opgeslagen, klik op het tabblad Gegevens en klik vervolgens op oplossen., De optimale oplossing en waarden worden weergegeven in de bijbehorende cellen. De optimale minimale kosten zijn us $ 0,90. Sara moet consumeren 3 eenheden van voedsel punt 2 en 1 eenheid van voedsel punt 3 voor de vereiste nutriëntengehalte tegen de minimale kosten. Dit Lost ons lineaire programma op.

Simplex methode

Simplex methode is een van de krachtigste & populaire methoden voor lineair programmeren. De simplex methode is een iteratieve procedure voor het verkrijgen van de meest haalbare oplossing., In deze methode blijven we de waarde van basisvariabelen transformeren om de maximale waarde voor de objectieve functie te krijgen.

een lineaire programmeerfunctie is in zijn standaardvorm als het de objectieve functie wil maximaliseren. onderworpen aan beperkingen,

. . . . . .

. . . . . .

waarbij en ., Na het toevoegen van slack variabelen is het overeenkomstige systeem van constraintvergelijking

. . . .

waarbij,

De variabelen, ………………. worden slack variabelen genoemd. Het zijn NIET-Negatieve getallen die worden toegevoegd om de ongelijkheden uit een vergelijking te verwijderen.

bovenstaande uitleg geeft de theoretische uitleg van de Simplex-methode., Nu, ik ga uitleggen hoe de Simplex methode te gebruiken in het echte leven met behulp van Excel.

voorbeeld: de advertentiealternatieven voor een bedrijf omvatten televisie -, kranten-en radio-advertenties. De kosten voor elk medium met zijn doelgroep dekking wordt hieronder gegeven.,

	Television	Newspaper	Radio
Cost per advertisement ($)	2000	600	300
Audience per advertisement	100,000	40,000	18,000

The local newspaper limits the number of advertisements from a single company to ten., Bovendien mag niet meer dan de helft van het totale aantal advertenties op de radio worden uitgezonden om de reclame over de drie soorten media in evenwicht te brengen. En ten minste 10% moet optreden op televisie. De wekelijkse reclame budget is $ 18.200. Hoeveel advertenties moeten worden uitgevoerd in elk van de drie soorten media om het totale publiek te maximaliseren?

oplossing: eerst ga ik mijn probleem formuleren voor een duidelijk begrip.,

Stap 1: Identificeer Beslissingsvariabelen

laat,, het totale aantal advertenties voor respectievelijk televisie, krant en radio weergeven.

Stap 2: objectieve functie

het doel van het bedrijf is om het publiek te maximaliseren. De objectieve functie wordt gegeven door:

Stap 3: schrijf de beperkingen

nu zal ik elke beperking één voor één noemen.

Het is duidelijk dat we een budgetbeperking hebben., Het totale budget dat kan worden toegewezen is $ 18.200. En de individuele kosten per televisie, krant en radio reclame is $2000, $600 en $300 respectievelijk. Dit kan worden weergegeven door de vergelijking,

voor een krantenadvertentie geldt een bovengrens voor het aantal advertenties tot 10. Mijn eerste beperkingen zijn,

de volgende beperking is het aantal advertenties op televisie., Het bedrijf wil ten minste 10% van de totale advertenties op televisie. Het kan dus worden weergegeven als:

de laatste beperking is het aantal advertenties op de radio mag niet meer dan de helft van het totale aantal advertenties zijn. Het kan worden weergegeven als

nu heb ik mijn lineaire programmeerprobleem geformuleerd. We gebruiken de simplex methode om dit op te lossen. Ik zal je één voor één door de Simplex methode leiden.

om te herhalen zijn alle beperkingen als volgt., I have simplified the last two equations to bring them in standard form.

We have a total of 4 equations. To balance out each equation, I am introducing 4 slack variables, , and .,

dus onze vergelijkingen zijn als volgt:

ik hoop dat u nu beschikbaar bent om het hele advertentieprobleem te begrijpen. Alle bovenstaande vergelijkingen zijn alleen voor uw beter begrip. Als je nu deze vergelijkingen oplost, krijg je de waarden voor X1= 4, X2= 10 en X3= 14.

bij het oplossen van de objectieve functie krijgt u de maximale wekelijkse publiek als 1.052.000., U kunt de tutorial hier volgen om de vergelijking op te lossen. Volg deze zelfstudie om een lineair programma in excel op te lossen.

Northwest Corner Method and Least Cost Method

6.1 Northwest Corner Method

de northwest corner method is een speciale methode die wordt gebruikt voor transportproblemen bij lineaire programmering. Het wordt gebruikt om de haalbare oplossing te berekenen voor het vervoer van goederen van de ene plaats naar de andere. Wanneer je een reëel probleem krijgt, waarbij vraag en aanbod uit één bron van verschillende bronnen betrokken zijn., Het gegevensmodel omvat het volgende:

• het niveau van vraag en aanbod bij elke bron wordt gegeven
• het eenheidstransport van een grondstof van elke bron naar elke bestemming

het model gaat ervan uit dat er slechts één grondstof is. De vraag naar die kan komen uit verschillende bronnen. Het doel is om te voldoen aan de totale vraag met minimale transportkosten. Het model is gebaseerd op de hypothese dat de totale vraag gelijk is aan het totale aanbod, dat wil zeggen dat het model in evenwicht is. Laten we dit begrijpen met behulp van een voorbeeld.,

voorbeeld: Er zijn 3 silo ‘ s nodig om aan de vraag van 4 walsgroepen te voldoen. (Een silo is een opslagruimte van de boerderij gebruikt om graan op te slaan en molen is een slijpfabriek voor granen).

oplossing: laten we begrijpen wat de bovenstaande tabel verklaart.

de kosten van het vervoer van Silo i naar Molen j worden gegeven door de kosten in elke cel die overeenkomen met het aanbod van elke silo 1 en de vraag in elke molen., Bijvoorbeeld, de kosten van het vervoer van Silo 1 naar Molen 1 is $10, van Silo 3 naar Molen 5 is $ 18. Het wordt ook gegeven de totale vraag & aanbod voor walserij en silo ‘ s. Het doel is om de minimale transportkosten zodanig te vinden dat aan de vraag naar alle molens wordt voldaan.

zoals de naam al doet vermoeden is de Northwest corner methode een methode voor het toewijzen van de eenheden vanaf de cel linksboven. De vraag naar Molen 1 is 5 en Silo 1 heeft een totaal aanbod van 15. Dus, 5 eenheden kunnen worden toegewezen aan Mill1 tegen een kostprijs van $ 10 per eenheid. Aan de vraag naar Millenium1 is voldaan., dan gaan we naar de cel linksboven van Molen 2. De vraag naar Molen 2 is 15 eenheden, die het kan krijgen 10 eenheden van Silo 1 tegen een kostprijs van $ 2 per eenheid en 5 eenheden van Silo 2 tegen een kostprijs van $7 per eenheid. Dan gaan we naar Molen 3, de noordwestelijke cel is S2M3. De vraag naar Molen 3 is 15 eenheden, die het kan krijgen van Silo 2 tegen een kostprijs van $ 9 per eenheid. Op weg naar de laatste Molen, Molen 4 heeft een vraag van 15 eenheden. Het krijgt 5 eenheden van een Silo 2 tegen een kostprijs van $ 20 per eenheid en 10 eenheden van Silo 3 tegen een kostprijs van $ 18 per eenheid.,

de totale vervoerskosten zijn:= 5*10+(2*10+7*5)+9*15+(20*5+18*10) = $520

6.2 Least Cost Method

Least Cost method is een andere methode om de meest haalbare oplossing voor een lineair programmeerprobleem te berekenen. Deze methode leidt nauwkeuriger resultaten af dan de methode van de noordwesthoek. Het wordt gebruikt voor transport-en productieproblemen. Om het simpel te houden leg ik het bovenstaande transportprobleem uit.,

volgens de least cost method start u vanuit de cel met de laagste eenheidskosten voor transport. Dus, voor het bovenstaande probleem, Ik leveren 5 eenheden van Silo 3 tegen een per-eenheid kosten van $ 4. Aan de vraag naar Millenium1 is voldaan. Voor Molen 2, leveren wij 15 eenheden van Silo 1 tegen een per eenheid kosten van $ 2. Dan voor Molen 3 leveren wij 15 eenheden van Silo 2 tegen een per-eenheid kosten van $ 9. Dan voor Molen 4 leveren wij 10 eenheden van Silo 2 tegen een per eenheid kosten van $ 20 en 5 eenheden van Silo 3 een $ 18 per eenheid., De totale transportkosten zijn $ 475.

de bovenstaande methode legt uit dat we onze kosten verder kunnen optimaliseren met de beste methode. Laten we dit controleren met Excel Solver. Solver is een ingebouwde add-on in Microsoft Excel. Het is een invoegtoepassing die beschikbaar is in Excel. Ga naar bestand->opties->add-ins->select solver->klik op Beheren->select solver->klik OK. Uw oplosser is nu toegevoegd in excel. U kunt het controleren onder de Data tab.,

het eerste wat ik ga doen is mijn gegevens in excel invoeren. Na het invoeren van de gegevens in excel, heb ik het totaal van C3:F3 berekend. Ook voor anderen. Dit wordt gedaan om de totale vraag van Silo 1 en anderen te nemen.

hierna breek ik mijn model in tweeën. De eerste tabel geeft me de geleverde eenheden en de tweede tabel geeft me de kosten per eenheid.,

nu ben ik bezig mijn totale kosten te berekenen, die zullen worden opgegeven per product van eenheidskosten en geleverde eenheden.

nu ga ik Solver gebruiken om mijn model te berekenen. Vergelijkbaar met de bovenstaande methode. Voeg de objectieve functie, variabele cellen, beperkingen toe.

nu is uw model klaar om opgelost te worden. Klik op oplossen en u krijgt uw optimale kosten., De minimale transportkosten zijn $ 435.

toepassingen van lineair programmeren

lineaire programmering en optimalisatie worden gebruikt in verschillende industrieën. De productie-en dienstverlenende industrie maakt regelmatig gebruik van lineair programmeren. In deze sectie gaan we kijken naar de verschillende toepassingen van lineaire programmering.

1. verwerkende industrie gebruikt lineaire programmering voor het analyseren van hun activiteiten in de toeleveringsketen. Hun motief is om de efficiëntie te maximaliseren met minimale werkingskosten., Volgens de aanbevelingen van het lineaire programmeermodel kan de fabrikant zijn opslagindeling opnieuw configureren, zijn personeelsbestand aanpassen en de knelpunten verminderen. Hier is een kleine magazijn case studie van Cequent een in de VS gevestigde bedrijf, bekijk deze video voor een meer duidelijk begrip.
2. lineair programmeren wordt ook gebruikt in georganiseerde retail voor het optimaliseren van schapruimte. Aangezien het aantal producten in de markt met sprongen is toegenomen, is het belangrijk om te begrijpen wat de klant wil., Optimalisatie wordt agressief gebruikt in winkels zoals Walmart, Hypercity, Reliance, Big Bazaar, enz. De producten in de winkel worden strategisch geplaatst rekening houdend met het patroon van de klant winkelen. Het doel is om het voor een klant gemakkelijk te maken om & de juiste producten te selecteren. Dit is onderhevig aan beperkingen zoals beperkte schapruimte, een verscheidenheid aan producten, enz.
3. optimalisatie wordt ook gebruikt voor het optimaliseren van Leveringsroutes. Dit is een uitbreiding van de populaire reizende verkoper probleem., De service industrie maakt gebruik van optimalisatie voor het vinden van de beste route voor meerdere verkopers reizen naar meerdere steden. Met behulp van clustering en hebzuchtige algoritme, de levering routes worden bepaald door bedrijven als FedEx, Amazon, enz. Het doel is om de operatie kosten en tijd te minimaliseren.
4. optimalisaties worden ook gebruikt in Machine Learning. Begeleid leren werkt op de basis van lineair programmeren. Een systeem wordt getraind om te passen op een wiskundig model van een functie van de gelabelde invoergegevens die waarden kunnen voorspellen van een onbekende testgegevens.,

De Toepassingen van lineair programmeren eindigen hier niet. Er zijn veel meer toepassingen van lineaire programmering in de echte wereld zoals toegepast door aandeelhouders, Sport, aandelenmarkten, enz. Ga verder en ontdek verder.

End Notes

ik hoop dat u dit artikel leuk vond. Ik heb geprobeerd alle basisbegrippen onder lineair programmeren uit te leggen. Als u twijfels of vragen hebt, aarzel dan niet om ze te posten in de commentaren sectie., Voor een eenvoudig begrip hebben we dit lange artikel opgesplitst in een korter cursusformaat – Linear Programming for Data Science Professionals

ik heb elk concept uitgelegd met een real-life voorbeeld. Ik wil dat je ze aan jouw kant probeert en praktijkervaring opdoet. Laat me weten wat je ervan vindt!

leer, wedijver, hack en word aangenomen!

u kunt dit artikel ook lezen op onze mobiele APP