Innledning
Optimalisering er livets vei. Vi alle har begrensede ressurser og tid, og vi ønsker å gjøre mest mulig ut av dem. Fra å bruke tiden produktivt å løse supply chain problemer for din bedrift – alt bruker optimalisering. Det er en spesielt interessant og relevant tema i data vitenskap.,
Det er også et veldig interessant tema – det starter med enkle problemer, men det kan bli svært komplekse. For eksempel deling av en sjokolade mellom søsken er en enkel optimalisering problem. Vi tror ikke på matematisk form mens du løser det. På den annen side, å utarbeide inventar og lager en strategi for e-handel kan være svært komplekse. Millioner av Skuer med forskjellige popularitet i forskjellige regioner for å bli levert i en definert tid og ressurser – du ser hva jeg mener!,
Lineær programmering (LP) er en av de enkleste måter å utføre optimalisering. Det hjelper deg med å løse noen svært komplekse optimalisering problemer ved å gjøre noen forenkle forutsetninger. Som analytiker, du er nødt til å komme på tvers av programmer og problemer å være løst ved Lineær Programmering.
For noen grunn, LP ikke får så mye oppmerksomhet som det fortjener mens læring data vitenskap. Så, jeg trodde la meg gjøre rettferdighet til denne fantastisk teknikk. Jeg bestemte meg for å skrive en artikkel som forklarer Lineær programmering i enkle engelsk., Jeg har holdt innhold så enkelt som mulig. Ideen er å komme i gang, og begeistret for Lineær Programmering.
Merk – Hvis du ønsker å lære dette i et kurs-format, vi har kuratert dette gratis kurset for deg – Lineær Programmering for Data Science Fagfolk
Tabell for Innhold
– >
- Hva er Lineær Programmering?,
- Grunnleggende Terminologier
- prosess for å definere et LP problem
- Løse Lineære Program med Grafisk Metode
- Løse Lineære Program ved hjelp av R
- Løse Lineære Program ved hjelp av OpenSolver
- Simplex Metoden
- Nordvestre Hjørnet Metode og Minst kostnadskrevende Metode
- Anvendelser av Lineær programmering
Hva er Lineær Programmering?
Nå, hva er lineær programmering? Lineær programmering er en enkel teknikk hvor vi viser komplekse sammenhenger gjennom lineære funksjoner, og deretter finne den optimale poeng., Viktige ord i den forrige setningen er avbildet. Den virkelige relasjoner kan være mye mer komplisert – men vi kan forenkle dem til å lineære relasjoner.
Anvendelser av lineær programmering er overalt rundt deg. Du bruker lineær programmering på personlig og profesjonell fronter. Du er ved hjelp av lineær programmering når du kjører fra hjem til arbeid og ønsker å ta den korteste ruten. Eller når du har et prosjekt levering du lage strategier for å gjøre ditt team til å jobbe effektivt on-time levering.,
Eksempel på en lineær programmering problem
La oss si at en FedEx levering mann har 6 pakker til å levere i løpet av en dag. Lageret ligger i punktet A. 6 levering destinasjoner er gitt ved U, V, W, X, Y og Z. tallene på linjene indikerer avstanden mellom byene. For å spare drivstoff og tid for levering personen ønsker å ta den korteste ruten.
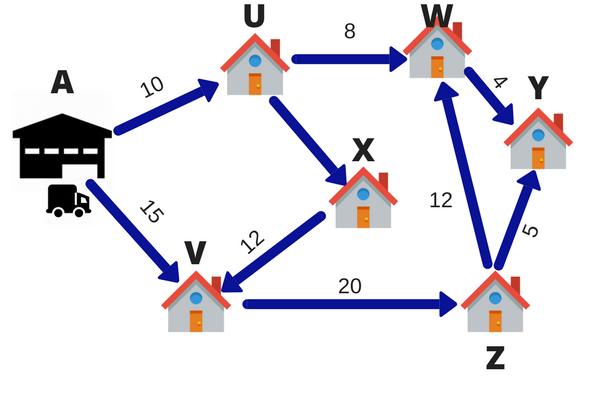
Så, levering person vil beregne forskjellige ruter som går til alle de 6 destinasjoner, og deretter komme opp med den korteste ruten., Denne teknikken med å velge den korteste ruten kalles lineær programmering.
I dette tilfellet målet for levering person er å levere pakken på tid i det hele tatt 6 destinasjoner. Prosessen med å velge den beste ruten er kalt Operasjon Forskning. Drift forskning er en tilnærming til beslutningstaking, noe som innebærer et sett av metoder for å drive et system. I eksempelet ovenfor, kan systemet mitt var Levering modell.
Lineær programmering brukes for å oppnå den mest optimale løsning for et problem med gitte begrensninger., I lineær programmering, vi formulerer vår virkelige problemet inn i en matematisk modell. Det innebærer en objektiv funksjon, lineære ulikheter med underlagt begrensninger.
Er lineær representasjon av de 6 punktene ovenfor representant for den virkelige verden? Ja og Nei. Det er en overforenkling som den virkelige ruten vil ikke være en rett linje. Det ville trolig ha flere svinger, U-svinger, signaler og trafikkork. Men med en enkel antakelse, vi har redusert kompleksiteten av problemet drastisk og er å skape en løsning som skal fungere i de fleste scenarier.,
Formulere et problem – La ‘ s produsere noen sjokolade
Eksempel: Vurdere en sjokolade produksjonsbedrift som produserer bare to typer sjokolade – A og B. Både sjokolade krever Melk og Choco bare. For å produsere hver enhet av A og B, følgende mengder er nødvendig:
- Hver enhet av En krever 1 enhet av Melk og 3 enheter av Choco
- Hver enhet av B krever 1 enhet av Melk og 2 enheter av Choco
selskapet kjøkken har en total av 5 enheter av Melk og 12 enheter Choco., På hvert salg, selskapet gjør et overskudd av
- Rs 6 per enhet A som selges
- Rs 5 per enhet B som selges.
Nå, selskapet ønsker å maksimere sin profitt. Hvor mange enheter av A og B skal det produsere henholdsvis?
Løsning: Det første jeg skal gjøre er å representere problemet i en tabellarisk form for bedre forståelse.,>
La det totale antall enheter produsert av A = X
La det totale antall enheter produsert av B være = Y
Nå, det samlede resultatet er representert ved Z
total fortjeneste selskapet gjør er gitt ved total antall enheter av A-og B-produsert multiplisert med dens per enhet resultat av Rs 6 og Rs 5 hhv.,
Resultat: Max Z = 6X+5Y
som betyr at vi har å maksimere Z.
selskapet vil prøve å produsere så mange enheter av A og B for å maksimere profitt. Men ressursene Melk og Choco er tilgjengelig i et begrenset beløp.
Som angitt i tabellen ovenfor, hver enhet av A og B krever 1 stk på Melk. Den totale mengden av Melk tilgjengelig er 5 enheter., Å representere denne matematisk,
X+Y ≤ 5
Også, hver enhet av A og B krever 3 enheter & 2 enheter av Choco henholdsvis. Den totale mengden av Choco tilgjengelig er 12 enheter. Å representere denne matematisk,
3X+2Y ≤ 12
Også verdier for enheter av En kan bare være heltall.,
Slik at vi har to begrensninger, X ≥ 0 & Y ≥ 0
For selskapet å få maksimal profitt over ulikhetene har til å være fornøyd.
Dette kalles å formulere en real-world problemet inn i en matematisk modell.
Vanlige terminologier som brukes i Lineær Programmering
La oss definere noen terminologier som brukes i Lineær Programmering ved hjelp av eksemplet ovenfor.
- Avgjørelse Variabler: beslutningen om variablene er de variablene som vil bestemme min utgang., De representerer min ultimate løsningen. For å løse ethvert problem, vi må først identifisere de vedtak variabler. For eksempelet ovenfor, er det totale antallet enheter for A og B som er merket med X & Y henholdsvis er min beslutning variabler.
- Målet Funksjon: Det er definert som målet for beslutninger. I eksempelet ovenfor, kan selskapet ønsker å øke det totale resultatet representert ved Z. Så, profitt er målet mitt funksjon.,
- Begrensninger: begrensninger restriksjoner eller begrensninger på avgjørelsen variabler. De vanligvis begrense verdien av vedtaket variabler. I eksemplet ovenfor er det begrensninger på tilgjengeligheten av ressurser Melk og Choco er mine begrensninger.
- Ikke-negativitet begrensning: For alle lineære programmer, avgjørelsen variabler bør du alltid ta med ikke-negative verdier. Dette betyr at verdiene for beslutning variabler bør være større enn eller lik 0.,
prosessen med å formulere en Lineær Programmering problem
La oss se på trinnene for å definere en Lineær Programmering generelt problem:
- Identifisere beslutning variabler
- Skriv målet funksjon
- Nevne begrensninger
- Eksplisitt staten ikke-negativitet begrensning
For et problem å være en lineær programmering problem, beslutningen om variabler, mål funksjon og rammer alle har til å være lineære funksjoner.,
Hvis alle tre betingelser er oppfylt, er det som kalles en Lineær Programmering Problem.
Løse Lineære Programmer med Grafisk Metode
Et lineært program kan løses ved hjelp av flere metoder. I dette avsnittet skal vi se på Grafisk metode for å løse et lineært program. Denne metoden er brukt for å løse en to-variabel lineær programmet. Hvis du har bare to beslutning variabler, bør du bruke grafisk metode for å finne den optimale løsningen.,
En grafisk metode innebærer å formulere et sett av lineære ulikheter underlagt begrensninger. Deretter ulikhetene er plottet på et X-Y-planet. Når vi har plottet inn alle ulikhetene på en graf for den kryssende regionen gir oss et mulig område. Det er mulig regionen forklarer hva alle verdier vår modell kan ta. Og det gir oss den optimale løsningen.
La oss forstå dette ved hjelp av et eksempel.
Eksempel: En bonde har nylig overtatt en 110 hektar stykke land., Han har bestemt seg for å dyrke Hvete og bygg på at landet. På grunn av kvaliteten på solen og regionens gode klima, hele produksjonen av Hvete og Bygg kan bli solgt.,h utvalg i 110 hektar, gitt kostnader, netto fortjeneste og arbeidskraft som trengs i henhold til de data som er vist nedenfor:
| Utvalg | Kostnader (Pris/Hektis) | Resultat etter skatt (Pris/Hektis) | Mann-dager/Hektis |
| Hvete | 100 | 50 | 10 |
| – Bygg | 200 | 120 | 30 |
bonden har et budsjett på US$10 000 og tilgjengelighet på 1 200 mann-dager under planlegging horisonten., Finne den optimale løsningen og optimal verdi.
Løsning: for Å løse dette problemet, først vi skal utforme vår lineære program.
Formulering av Lineære Problem
Trinn 1: Identifisere beslutning variabler
totale areal for dyrking av Hvete = X (i dekar)
totale areal for dyrking av Bygg = Y (i dekar)
X og Y er min beslutning variabler.
Trinn 2: Skriv inn mål funksjon
Siden produksjonen fra hele landet kan selges i markedet. Bonden ønsker å maksimere profitt for hans totale produksjon., Vi er gitt som netto gevinst for både Hvete og Bygg. Bonden tjener et netto overskudd på US$50 for hver hektar av Hvete og US$120 for hvert Bygg.
Vår målsetning funksjon (gitt ved Z) er, Max Z = 50X + 120Y
Trinn 3: Skrive begrensninger
1. Det er gitt at bonden har et samlet budsjett på US$10,000. Kostnaden ved å produsere Hvete og Bygg per hektar er også gitt til oss. Vi har et øvre tak på den totale kostnaden brukt av bonden. Så vår ligningen blir:
100X + 200Y ≤ 10,000
2., Den neste begrensningen er øvre tak på tilgjengeligheten av totalt antall mann-dager for planleggingshorisont. Det totale antall av mann-dager tilgjengelig 1200. Som angitt i tabellen, har vi fått mannen-dager per hektar for Hvete og Bygg.
10X + 30Y ≤ 1200
3. Den tredje begrensningen er det totale arealet til stede for plantasjen. Totalt tilgjengelig areal er 110 hektar., Slik at ligningen blir,
X + Y ≤ 110
Trinn 4: ikke-negativitet begrensning
verdiene av X og Y vil være større enn eller lik 0. Dette går uten å si.
X ≥ 0, Y ≥ 0
Vi har formulert vår lineære program. Det er på tide å løse det.
Løse en LP gjennom Grafisk metode
Siden vi vet at X, Y ≥ 0. Vi vil vurdere bare de første kvadrant.
for Å legge til grafen for over ligninger, første jeg vil forenkle alle ligningene.,
100X + 200Y ≤ 10,000 kan forenkles til X + 2Y ≤ 100 ved å dividere med 100.
10X + 30Y ≤ 1200 kan forenkles til X + 3Y ≤ 120 ved å dividere med 10.
Den tredje ligningen er i sin forenklede form, X + Y ≤ 110.
Plot de første 2 linjer på en graf i første kvadrant (som vist nedenfor)
optimal mulig løsning er oppnådd i skjæringspunktet der den økonomiske & mann-dager begrensninger er aktiv., Dette betyr at punktet som ligningene X + 2Y ≤ 100 og X + 3Y ≤ 120 snitt gir oss den optimale løsningen.
verdiene for X og Y som gir den optimale løsning er på (60,20).
for Å maksimere profitt bonden skal produsere Hvete og Bygg i 60 dekar og 20 hektar land hhv.,
maksimal profitt selskapet vil få,
Maks Z = 50 * (60) + 120 * (20)
= US$(5400 o / min

Merk: Alt lært her har også vært undervist i kurset format i dette gratis kurs – Lineær Programmering for Data Science Fagfolk
Løse Lineære Program ved Hjelp av R
R er en åpen-kilde verktøy som er svært populær blant de data som forskere for viktige data science oppgaver. Utfører lineær programmering er veldig enkelt, og vi kan oppnå en optimal løsning i svært få trinn. Kom la oss lære.,
Eksempel: En leken produksjon organisasjonen produserer to typer leker A og B. Begge lekene er solgt på Rs.25 og Rs.20 kroner. Det er 2000 ressurs-enheter tilgjengelig hver dag som leketøy-En krever 20 enheter mens leken B krever 12 enheter. Begge disse lekene krever en produksjonstid på 5 minutter. Samlede arbeidstid er 9 timer en dag. Hva som bør være produksjon mengde for hvert av rørene for å maksimere fortjenesten?
Her:
målet funksjonen er:
Maks.,Z=25x+20y
der x er enheter av pipe En
y er enheter av rør B
Begrensninger:
20 x+12y<=2000
5x+5y<=540
La oss se koden del nå:
Output
Derfor fra utgang, vi ser at organisasjonen skal produsere 88 enheter av leketøy og En 20 enheter av leketøy B og maksimal gevinst for organisasjonen vil være Rs.2600.,
Løse Lineære Program ved hjelp av OpenSolver
I virkeligheten, et lineært program kan inneholde 30 til 1000 variabler og løse det enten Grafisk eller Algebraically er nesten umulig. Selskapene bruker vanligvis OpenSolver å takle disse problemer i den virkelige verden. Her jeg skal ta deg gjennom trinnene for å løse et lineært program ved hjelp av OpenSolver.
OpenSolver er en åpen-kilde lineær og optimizer for Microsoft Excel. Det er en avansert versjon av en innebygd Excel Solver. Du kan laste ned OpenSolver her og følg installasjonsveiledningen.,
jeg vil at du skal få praktisk kunnskap i bruk av OpenSolver. Så, for en klar forståelse, vil jeg forklare det med et eksempel.
Eksempel: Nedenfor er det en diett diagram som gir meg kalorier, protein, karbohydrater og fett innhold for 4 matvarer. Sara ønsker en diett med minimale kostnader., The diet chart is as follows:
| Food Item 1 | Food Item 2 | Food Item 3 | Food Item 4 | |
| Calories | 400 | 200 | 150 | 500 |
| Protien (in grams) | 3 | 2 | 0 | 0 |
| Carbohydrates ( in grams) | 2 | 2 | 4 | 4 |
| Fat (in grams) | 2 | 4 | 1 | 5 |
| Cost | $0.50 | $0.20 | $0.,30 | $0.80 |
diagrammet gir næringsrikt innhold samt per-kostnad for hver mat element. Dietten må planlegges på en slik måte at det bør inneholde minst 500 kalorier, 6 gram protein, 10 gram karbohydrater og 8 gram fett.
Løsning: for det Første, jeg skal formulere min lineær program i et regneark.
- Trinn 1: Identifisere beslutning variabler. Her er min beslutning om variablene er mat. Legge til topp., For testformål, vi går inn i vilkårlige verdier. La oss si, Sara bruker 3 enheter av Mat post 1, 0 enhet av Mat Punkt 2, 1 stykk av Mat Punkt 3 og 0 enhet av Mat, Punkt 4. Disse kalles variabel celler.

- Trinn 2: Nå vil vi skrive våre mål funksjon. For diett for å bli optimal må vi ha minimum kostnad sammen med nødvendig kalorier, protein, karbohydrater og fett.

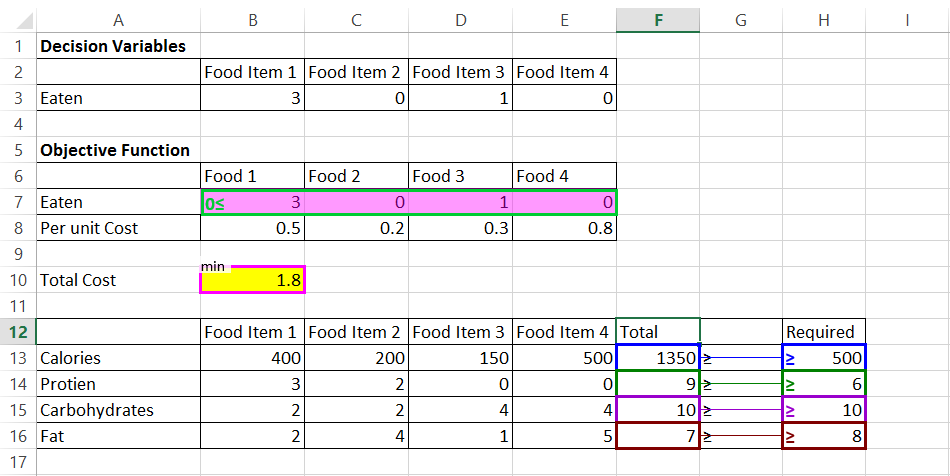
I celle B7:E7 vi tar referansen til antall enheter., Og i celle B8:E8 vi satte per-kostnad for hver mat element.
I celle B10, vi vil den totale kostnaden av kostholdet. De totale kostnadene er gitt ved sumproduct av antall enheter spist og per-kostnad. Sumproduct er gitt ved = B7*B8+C7*C8+D7*D8+E7*E8. La oss se på dette i et regneark.

- Trinn 3: Nå vil vi angi begrensninger. Kolonne F inneholder en total av kalorier, protein, karbohydrater og fett., Det totale antall av kaloriinntaket i gitt ved sumproduct antall matvarer spist og kalori konsumert per mat element. For celle F13= Sumprodcut($B$7:$F$7, B13:F13). Tilsvarende for andre. Kolonne G gir ulikheten siden problemet krav Kalorier, Protein, Karbohydrat og Fett til å være minst 500, 6, 10 og 8, henholdsvis. Kolonne H gir de nødvendige næringsstoffer innhold.

- Trinn 4: Nå, vi vil gå inn i en Lineær programmet til brukeren. Nå, når du har installert OpenSolver., Når du klikker på kategorien Data, på høyre side vil du se Modell. Klikk på modellen, og skriv deretter inn verdiene én etter én. For det første, vi vil gå inn i mål funksjon,$B10 jeg.e i mål celle. Velg minimer fordi vi ønsker å minimere diett kostnader.

- Trinn 5: legg inn beslutning variabler i variabelen celler.

- Trinn 6: Nå, vil vi legge begrensninger. Den første begrensningen er F13 ≥ H13. Legge til alle de begrensninger én etter én.,
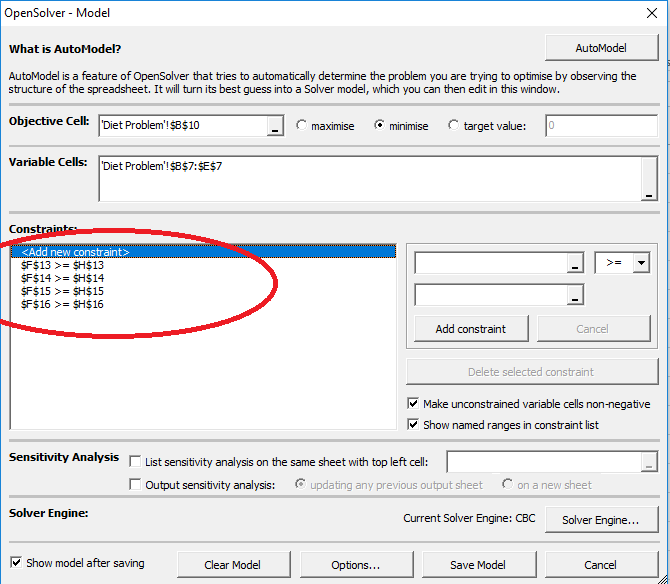
- Trinn 7: Nå må du angi en viktig begrensning. Den ikke-negativitet begrensning. Alle vedtak variabler vil være større enn 0.

- Trinn 8: Nå, klikker du på Lagre-Modellen for å fullføre modellering prosess. Når du lagrer modellen, det vil se ut noe som dette.
- Trinn 9: Når modellen er lagret klikk på Data-fanen og deretter klikke løse., Den optimale løsningen og verdier vises i den tilsvarende celler. Den optimale minimum kostnad er US$0.90. Sara bør spise 3 enheter av Mat Punkt 2 og 1 enhet av Mat Punkt 3 for nødvendige næringsstoffer innhold på minimum kostnad. Dette løser våre lineær programmet.

Simplex Metoden
Simplex-Metoden er en av de mektigste & populære metoder for lineær programmering. Den simplex-metoden er en iterativ prosedyre for å få mest mulig løsning., På denne måten kan vi holde transformere verdien av grunnleggende variabler for å få maksimal verdi for objektiv funksjon.
En lineær programmering funksjon er i standard form hvis den søker å maksimere mål funksjon.  underlagt begrensninger,
underlagt begrensninger,

. . . . . .
. . . . . .

hvor ![]() og
og ![]() ., Etter å ha lagt slakk variabler, tilsvarende system av tvang ligningen,
., Etter å ha lagt slakk variabler, tilsvarende system av tvang ligningen,
![]()
![]()
. . . .
![]() hvor
hvor ![]()
variablene,![]()
![]() ……………….
……………….![]() kalles slakk variabler. De er ikke-negative tall som er lagt til for å fjerne ulikheter fra en ligning.
kalles slakk variabler. De er ikke-negative tall som er lagt til for å fjerne ulikheter fra en ligning.
ovenstående redegjørelse gir en teoretisk forklaring av simplex-metoden., Nå, jeg skal forklare hvordan du bruker simplex-metoden i det virkelige liv ved hjelp av Excel.
Eksempel: reklame alternativer for et selskap inkluderer tv, avis og radio reklame. Kostnaden for hvert medium med sitt publikum dekning er gitt nedenfor.,
| Television | Newspaper | Radio | |
| Cost per advertisement ($) | 2000 | 600 | 300 |
| Audience per advertisement | 100,000 | 40,000 | 18,000 |
The local newspaper limits the number of advertisements from a single company to ten., Videre, for å balansere reklame blant de tre typer media, ikke mer enn halvparten av det totale antall annonser skal skje på radioen. Og minst 10% skal skje på tv. Den ukentlige annonsering budsjett er $18,200. Hvor mange annonser som skal kjøres i hver av de tre typer medier for å maksimere den totale publikum?
Løsning: Først kommer jeg til å formulere problemet mitt for en klar forståelse.,
Trinn 1: Identifisere Beslutning Variabler
La ![]() ,
,![]() ,
, ![]() representerer totalt antall annonser for fjernsyn, avis og radio henholdsvis.
representerer totalt antall annonser for fjernsyn, avis og radio henholdsvis.
Trinn 2: Mål Funksjon
målet for selskapet er å få størst mulig publikum. Målet funksjon er gitt ved:
![]()
Trinn 3: Skriv ned de begrensninger
Nå, vil jeg nevne hver begrensning én etter én.
Det er helt klart gitt at vi har et budsjett for tvang., Det totale budsjettet som kan være tilordnet $18,200. Og den individuelle kostnader per-tv, avis og radio reklame er $2000, $600 og kr 300 kroner. Dette kan være representert ved ligningen,
![]()
For en avis annonse, for det er en øvre grense på antall annonser til 10. Min første begrensninger er, ![]()
Den neste begrensningen er antall reklame på tv., Selskapet ønsker at minst 10% av den totale annonser for å være på tv. Så, det kan bli representert som:
![]()
Den siste begrensningen er antall annonser på radio kan ikke være mer enn halvparten av det totale antall annonser. Det kan være representert
![]()
Nå, jeg har formulert min lineær programmering problem. Vi bruker simplex metoden for å løse dette. Jeg vil ta deg gjennom simplex-metoden, en etter en.
for Å gjenta alle de begrensninger som følger., I have simplified the last two equations to bring them in standard form.
![]()
![]()
![]()
![]()
We have a total of 4 equations. To balance out each equation, I am introducing 4 slack variables,![]()
![]() ,
, ![]() and
and ![]() .,
.,
Så vår ligningene er som følger:
![]()
![]()
![]()
![]()
Jeg håper nå du er tilgjengelig for å gjøre følelse av hele annonsering problem. Alle de ovennevnte ligningene er kun til bedre forståelse. Nå hvis du løse disse ligningene, vil du få verdiene for X1= 4, X2= 10 og X3= 14.
På for å løse målet funksjon du vil få maksimal ukentlig publikum som 1,052,000., Du kan følge veiledningen her for å løse ligningen. For å løse et lineært program i excel, kan du følge denne opplæringen.
Nordvestre Hjørnet Metode og Minst kostnadskrevende Metode
6.1 Nordvestre Hjørnet Metode
Det nordvestlige hjørnet metoden er en spesiell type metode som brukes for transport av problemer i lineær programmering. Det er brukt til å beregne mulig løsning for transport av varer fra ett sted til et annet. Når du er gitt en reell problem, som innebærer tilbud og etterspørsel fra en kilde til en annen kilder., Data modellen inneholder følgende:
- nivået av tilbud og etterspørsel på hver kilde er gitt
- enhet transport av en vare fra hver kilde til hver destinasjon
modellen forutsetter at det er bare én vare. Etterspørselen etter som kan komme fra forskjellige kilder. Målet er å oppfylle den totale etterspørselen med minimum transportkostnader. Modellen er basert på hypotesen om at den totale etterspørselen er lik den totale tilførsel, jeg.e modellen er balansert. La oss forstå dette ved hjelp av et eksempel.,
Eksempel: Tenk at det er 3 siloer som er nødvendig for å tilfredsstille etterspørselen fra 4 mills. (En silo er et område for lagring av gården som brukes til å lagre korn og Mølle er en sliping fabrikk for korn).

Løsning: La oss forstå hva som tabellen ovenfor forklarer.
kostnadene for transport fra Silo jeg til Mill j er gitt av kostnadene i hver celle svarer til tilbudet fra hver silo 1 og etterspørselen ved hver Mølle., For eksempel kostnaden ved å transportere fra Silo 1 til 1 Mill er $10, fra Silo 3 til 5 Mill er $18. Det er også gitt den totale etterspørselen & forsyning for mill og siloer. Målet er å finne den minimale transportkostnader slik at etterspørselen etter alle fabrikkene er fornøyd.
Som navnet antyder Nordvestre hjørnet metode er en metode for å tildele enhetene starter fra den øverste venstre cellen. Behovet for Mill 1 er 5 og Silo 1 har en total tilførsel av 15. Så, 5 enheter kan være allokert til Mill1 til en kostnad av $10 per enhet. Etterspørselen etter Mill1 er oppfylt., deretter flytter vi til den øverste venstre cellen av 2 Mill. Etterspørselen etter 2 Mill er 15 enheter, som det kan få 10 enheter fra Silo 1 til en kostnad av $2 per enhet og 5 enheter fra Silo 2 til en kostnad av $7 per enhet. Deretter flytter vi inn 3 Mill, nordvest celle er S2M3. Etterspørselen etter 3 Mill er 15 enheter, der det kan komme fra Silo 2 til en kostnad av $9 per enhet. Flytte til den siste Mill Mill 4 har en etterspørsel av 15 enheter. Det vil bli 5 enheter fra en Silo 2 til en kostnad av $20 per enhet og 10 enheter fra Silo 3 til en kostnad av $18 per enhet.,
Den totale kostnadene for transport er = 5*10+(2*10+7*5)+9*15+(20*5+18*10) = $520

6.2 Minst kostmetoden
Minst Kost-metoden er en annen metode for å beregne den mest mulig løsning for en lineær programmering problem. Denne metoden stammer mer nøyaktige resultater enn Nordvestre hjørnet metode. Det er brukt til transport og produksjon problemer. For å holde det enkelt, jeg forklarer over transport problemet.,

i Henhold til minst kostnad metoden, kan du starte fra cellen som inneholder minst kostnad for transport. Så, for det foregående problemet, jeg levere 5 enheter fra Silo 3 på en per-enhet kostnad på $4. Etterspørselen etter Mill1 er oppfylt. For Mill 2, som vi leverer til 15 enheter fra Silo 1 på en per enhet kostnad på $2. Så For 3 Mill som vi leverer til 15 enheter fra Silo 2 på en per-enhet kostnad på $9. Så for Mill 4 vi leverer 10 enheter fra Silo 2 på en per enhet kostnad på $20 og 5 enheter fra Silo 3 en $18 per enhet., Den totale transportkostnader er $475.
Vel, metoden ovenfor forklarer vi kan optimalisere kostnadene våre videre med den beste metoden. La oss sjekke dette ved hjelp av Excel Solver. Solver er en innebygd add-on i Microsoft Excel. Det er en add-i plug tilgjengelig i Excel. Gå til fil->alternativer->add-ins->velg solver->klikk på administrer->velg solver->klikk på Ok. Din solver er nå lagt i excel. Du kan sjekke det under kategorien Data.,
Det første jeg skal gjøre er å taste inn mine data i excel. Når du har lagt inn data i excel, jeg har beregnet totalt C3:F3. Tilsvarende for andre. Dette er gjort for å ta den totale etterspørselen fra Silo 1 og andre.

Etter dette, jeg skal bryte min modell i to. Den første tabellen gir meg enheter som leveres og den andre tabellen gir meg kostnad.,

Nå er jeg beregning av min totale kostnadene som vil bli gitt ved Sumproduct av kostnad og enheter som leveres.

Nå jeg skal bruke Solver til å regne ut min modell. Lik den ovennevnte metoden. Legg til målet funksjon, variabel celler, begrensninger.

Nå modellen er klar til å bli løst. Klikk på løse, og du vil få optimale kostnaden., Minimum transport kostnaden er $435.

Anvendelser av Lineær Programmering
Lineær programmering og Optimalisering er brukt i ulike bransjer. Produksjon og service industrien bruker lineær programmering på en jevnlig basis. I dette avsnittet skal vi se på de ulike anvendelser av Lineær programmering.
- Industrien bruker lineær programmering for å analysere deres supply chain operasjoner. Deres motiv er å maksimere effektiviteten med et minimum av drift kostnader., I henhold til anbefalinger fra lineær programmering modell, produsenten kan omkonfigurere sine lagring layout, justere sine ansatte og redusere flaskehalser. Her er et lite Lager case-studie av Cequent en USA-basert selskap, se denne videoen for en mer klar forståelse.
- Lineær programmering er også brukt i organisert detaljhandel for hylleplass optimalisering. Siden antallet av produkter i markedet har økt i sprang og grensene, er det viktig å forstå hva kunden vil ha., Optimalisering er aggressivt brukes i butikker som Walmart, Hypercity, Tillit, Store Basaren, etc. Produktene i butikken er plassert strategisk for å holde i tankene kunden shopping mønster. Målet er å gjøre det enkelt for en kunde å finne & velge de riktige produktene. Dette er underlagt begrensninger som begrenset hylleplass, et utvalg av produkter, osv.
- Optimalisering er også brukt til å optimalisere Levering Ruter. Dette er en videreføring av den populære traveling salesman problem., Tjenesten industrien bruker optimalisering for å finne den beste ruten for flere selgere som reiser til flere byer. Med hjelp av klynging og grådige algoritmen, levering ruter er besluttet av selskaper som FedEx, Amazon, etc. Målet er å minimere bruk av tid og kostnader.
- Optimaliseringer er også brukt i maskinlæring. Overvåket Læring fungerer på det grunnleggende av lineær programmering. Et system er opplært til å passe på en matematisk modell av en funksjon fra merket input-data som kan forutsi verdier fra en ukjent test data.,
Vel, anvendelser av Lineær programmering stopper ikke her. Det er mange flere anvendelser av lineær programmering i den virkelige verden som anvendes av Aksjonærer, Idrett, Lager Markeder, osv. Gå på og utforske videre.
Avslutt Notater
jeg håper du likte å lese denne artikkelen. Jeg har prøvd å forklare alle de grunnleggende konseptene under lineær programmering. Hvis du er i tvil eller spørsmål kan du føle deg fri til å poste dem i kommentarfeltet., For enkel forståelse, har vi brutt denne lange artikkelen i en kortere kurs format – Lineær Programmering for Data Science Fagfolk
jeg har forklart hvert begrep med en ekte liv eksempel. Jeg vil at du skal prøve dem på slutten, og få hands-on erfaring. La meg få vite hva du synes!
finn ut, konkurrere, hack og få leid!
Du kan også lese denne artikkelen om vår Mobil-APP
