introduktion
optimering er livsstilen. Vi har alle begrænsede ressourcer og tid, og vi ønsker at få mest muligt ud af dem. Fra at bruge din tid produktivt til at løse forsyningskædeproblemer for din virksomhed-alt bruger optimering. Det er et særligt interessant og relevant emne inden for datavidenskab.,
det er også et meget interessant emne – Det starter med enkle problemer, men det kan blive meget komplekst. For eksempel er deling af en bar chokolade mellem søskende et simpelt optimeringsproblem. Vi tænker ikke matematisk, mens vi løser det. På den anden side kan udformning af lager-og lagerstrategi for en e-tailer være meget kompleks. Millioner af SKU ‘ er med forskellig popularitet i forskellige regioner, der skal leveres i defineret tid og ressourcer – du ser hvad jeg mener!,
lineær programmering (LP) er en af de enkleste måder at udføre optimering på. Det hjælper dig med at løse nogle meget komplekse optimeringsproblemer ved at lave et par forenklende antagelser. Som analytiker er du bundet til at støde på applikationer og problemer, der skal løses ved lineær programmering.
af en eller anden grund får LP ikke så meget opmærksomhed, som den fortjener, mens man lærer datavidenskab. Så, jeg troede, lad mig gøre retfærdighed over for denne fantastiske teknik. Jeg besluttede at skrive en artikel, der forklarer lineær programmering på simpelt engelsk., Jeg har holdt indholdet så enkelt som muligt. Ideen er at få dig i gang og begejstret for lineær programmering.
Bemærk – Hvis du vil lære dette i et kursusformat, har vi kurateret dette gratis kursus for dig-Lineær Programmering for fagfolk inden for datavidenskab
Indholdsfortegnelse
- hvad er lineær programmering?,
- Grundlæggende Terminologier
- processen med at definere en LP-problem
- Løse Lineære Program med Grafisk Metode
- Løse Lineære Program ved hjælp af R
- Løse Lineære Program ved hjælp af OpenSolver
- Simplex-Metode
- Nordvestlige Hjørne Metode og Mindst Omkostninger Metode
- Anvendelser af Lineær programmering
Hvad er Lineær Programmering?
Hvad er nu lineær programmering? Lineær programmering er en simpel teknik, hvor vi skildrer komplekse relationer gennem lineære funktioner og derefter finder de optimale punkter., Det vigtige ord i den foregående sætning er afbildet. De virkelige forhold kan være meget mere komplekse-men vi kan forenkle dem til lineære forhold.
anvendelser af lineær programmering er overalt omkring dig. Du bruger lineær programmering på personlige og professionelle fronter. Du bruger lineær programmering, når du kører hjemmefra til arbejde og ønsker at tage den korteste rute. Eller når du har en projektlevering, laver du strategier for at få dit team til at arbejde effektivt til levering til tiden.,
eksempel på et lineært programmeringsproblem
lad os sige, at en fede. – leveringsmand har 6 pakker, der skal leveres på en dag. Lageret er placeret på punkt A. de 6 leveringsdestinationer er givet af U, V,., Y, Y og.. tallene på linjerne angiver afstanden mellem byerne. For at spare på brændstof og tid ønsker leveringspersonen at tage den korteste rute.
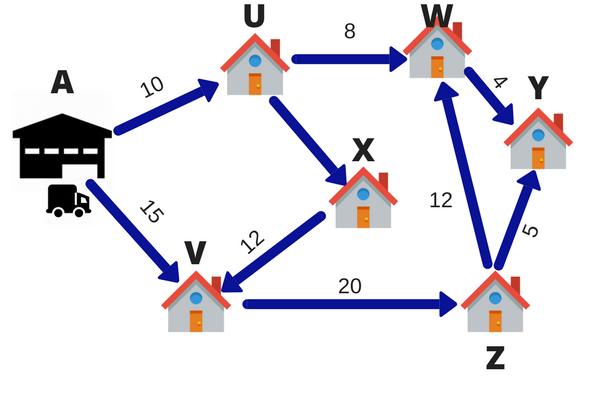
Så, levering person vil beregne forskellige ruter for at gå til alle de 6 destinationer, og derefter komme op med den korteste rute., Denne teknik til at vælge den korteste rute kaldes lineær programmering.
i dette tilfælde er leveringspersonens mål at levere pakken til tiden på alle 6 destinationer. Processen med at vælge den bedste rute kaldes Operation Research. Operation forskning er en tilgang til beslutningstagning, som indebærer et sæt metoder til at drive et system. I ovenstående eksempel var mit system leveringsmodellen.
lineær programmering bruges til at opnå den mest optimale løsning til et problem med givne begrænsninger., I lineær programmering formulerer vi vores virkelige problem til en matematisk model. Det indebærer en objektiv funktion, lineære uligheder med forbehold af begrænsninger.
er den lineære repræsentation af de 6 punkter ovenfor repræsentative for den virkelige verden? Ja og nej. Det er en forenkling, da den virkelige rute ikke ville være en lige linje. Det ville sandsynligvis have flere sving, U-sving, signaler og trafikpropper. Men med en simpel antagelse har vi reduceret kompleksiteten af problemet drastisk og skaber en løsning, der skal fungere i de fleste scenarier.,
formulering af et problem – lad os fremstille nogle chokolader
eksempel: overvej et chokoladeproduktionsfirma, der kun producerer to typer chokolade – A og B. Begge chokolader kræver kun mælk og Choco. Til at fremstille hver enhed af A og B, følgende mængder, der er nødvendige:
- Hver enhed af A kræver 1 enhed af Mælk og 3 enheder af Choco
- Hver enhed af B kræver 1 enhed af Mælk og 2 enheder af Choco
virksomheden køkken har en total af 5 enheder af Mælk og 12 enheder af Choco., Ved hvert salg opnår virksomheden et overskud på
- Rs 6 pr.solgte enhed
- RS 5 pr. solgte enhed B.
nu ønsker virksomheden at maksimere sin fortjeneste. Hvor mange enheder af A og B skal det producere henholdsvis?
løsning: det første jeg skal gøre er at repræsentere problemet i en tabelform for bedre forståelse.,>
Lad det samlede antal af enheder, der er fremstillet af Et = X
Lad det samlede antal enheder, der produceres af B være = Y
Nu, det samlede resultat er repræsenteret ved Z
Det samlede overskud, som virksomheden gør, er givet ved det samlede antal enheder, der er A-og B-produceret ganget med sin pr-enhed fortjeneste af Rs 6 og Rs 5 hhv.,
Resultat: Max Z = 6X+5Y
, som betyder, at vi er nødt til at maksimere Z.
vil virksomheden forsøge at producere så mange enheder af A og B for at maksimere profit. Men ressourcerne mælk og Choco er tilgængelige i et begrænset beløb.
ifølge ovenstående tabel kræver hver enhed af A og B 1 enhed mælk. Den samlede mængde mælk til rådighed er 5 enheder., For at repræsentere dette matematisk,
X+Y ≤ 5
Også, at hver enhed af A-og B-kræver 3 enheder & 2 enheder af Choco hhv. Den samlede mængde Choco til rådighed er 12 enheder. For at repræsentere dette matematisk,
3.+2Y 12 12
værdierne for enheder af A kan også kun være heltal.,
så vi har yderligere to begrænsninger, more 0 0 & Y 0 0
for at virksomheden kan opnå maksimal fortjeneste, skal ovennævnte uligheder opfyldes.
dette kaldes formulering af et problem i den virkelige verden til en matematisk model.
almindelige terminologier anvendt i lineær programmering
lad os definere nogle terminologier anvendt i Lineær Programmering ved hjælp af ovenstående eksempel.
- Beslutningsvariabler: beslutningsvariablerne er de variabler, der bestemmer min output., De repræsenterer min ultimative løsning. For at løse ethvert problem skal vi først identificere beslutningsvariablerne. For ovenstående eksempel er det samlede antal enheder For A og B betegnet med respectively & y henholdsvis mine beslutningsvariabler.
- objektiv funktion: det defineres som målet om at træffe beslutninger. I ovenstående eksempel ønsker virksomheden at øge det samlede overskud repræsenteret af.. så fortjeneste er min objektive funktion.,
- begrænsninger: begrænsningerne er begrænsningerne eller begrænsningerne for beslutningsvariablerne. De begrænser normalt værdien af beslutningsvariablerne. I ovenstående eksempel er grænsen for tilgængeligheden af ressourcer mælk og Choco mine begrænsninger.
- ikke-negativitetsbegrænsning: for alle lineære programmer skal beslutningsvariablerne altid tage ikke-negative værdier. Dette betyder, at værdierne for beslutningsvariabler skal være større end eller lig med 0.,
processen med at formulere en Lineær Programmering problem
Lad os se på det trin for at definere en Lineær Programmering problem generisk:
- Identificere beslutning variabler
- Skriv den objektive funktion
- Nævne begrænsninger
- Udtrykkeligt, at den ikke-negativitet begrænsning
For et problem, til at være en lineær programmering problem, afgørelsen variabler, mål, funktion og begrænsninger, der alle er nødt til at være lineære funktioner.,
hvis alle tre betingelser er opfyldt, kaldes det et lineært programmeringsproblem.
Løs lineære programmer ved grafisk metode
et lineært program kan løses ved flere metoder. I dette afsnit skal vi se på den grafiske metode til løsning af et lineært program. Denne metode bruges til at løse et to-variabelt lineært program. Hvis du kun har to beslutningsvariabler, skal du bruge den grafiske metode til at finde den optimale løsning.,
en grafisk metode indebærer formulering af et sæt lineære uligheder underlagt begrænsningerne. Derefter tegnes ulighederne på et YY-plan. Når vi har plottet alle uligheder på en graf den skærende region giver os en mulig region. Den gennemførlige region forklarer, hvad alle værdier vores model kan tage. Og det giver os også den optimale løsning.
lad os forstå dette ved hjælp af et eksempel.
eksempel: en landmand har for nylig erhvervet et stykke jord på 110 hektar., Han har besluttet at dyrke hvede og byg på dette land. På grund af solens kvalitet og regionens fremragende klima kan hele produktionen af hvede og byg sælges.,h udvalg på 110 hektar, i betragtning af de omkostninger, netto overskud og arbejdskraft krav i henhold til de data, der vises nedenfor:
| Række | Omkostninger (Pris/Hec) | Net Profit (Pris/Hec) | Mand-dage/Hec |
| Hvede | 100 | 50 | 10 |
| Byg | 200 | 120 | 30 |
landmanden har et budget på US$10.000 og tilgængelighed på 1.200 mand-dage i planlægningsperioden., Find den optimale løsning og den optimale værdi.
løsning: for at løse dette problem skal vi først formulere vores lineære program.
formulering af lineært Problem
Trin 1: Identificer beslutningsvariablerne
det samlede areal for dyrkning af hvede=. (i hektar)
det samlede areal for dyrkning af byg = Y (i hektar)
Step og Y er mine beslutningsvariabler.
Trin 2: Skriv den objektive funktion
da produktionen fra hele jorden kan sælges på markedet. Landmanden ønsker at maksimere overskuddet for hans samlede produktion., Vi får nettoresultat for både hvede og byg. Landmanden tjener et nettoresultat på US$50 for hver hektar hvede og US$120 for hver Byg.
vores objektive funktion (givet af Z) er, Ma. = =50. + 120Y
Trin 3: skrivning af begrænsningerne
1. Det er givet, at landmanden har et samlet budget på US $ 10.000. Omkostningerne ved produktion af hvede og byg per hektar er også givet til os. Vi har en øvre grænse på de samlede omkostninger, som landmanden bruger. Så vores ligning bliver:
100. + 200Y 10,000 10,000
2., Den næste begrænsning er den øverste hætte på tilgængeligheden af det samlede antal manddage for planlægningshorisonten. Det samlede antal man-dage til rådighed er 1200. I henhold til tabellen får vi manddage pr.hektar for hvede og byg.
10X + 30Y ≤ 1200
3. Den tredje begrænsning er det samlede areal til stede for plantagen. Det samlede tilgængelige areal er 110 hektar., Så ligningen bliver,
. + y 110 110
Trin 4: ikke-negativitetsbegrænsningen
værdierne for 0 og Y vil være større end eller lig med 0. Det siger sig selv.
X ≥ 0, Y ≥ 0
Vi har formuleret vores lineære program. Det er på tide at løse det.
løsning af en LP gennem grafisk metode
da vi ved, at Y, Y 0 0. Vi vil kun overveje den første kvadrant.
for at plotte for grafen for ovenstående ligninger, vil jeg først forenkle alle ligningerne.,
100 + + 200Y 10,000 10.000 kan forenkles til + + 2Y 100 100 ved at dividere med 100.
10 + + 30Y 10 1200 kan forenkles til + + 3Y 120 120 ved at dividere med 10.
den tredje ligning er i sin forenklede form, + + y 110 110.
Plot af de første 2 linjer på en graf i første kvadrant (som vist nedenfor)
Den optimale mulig løsning er opnået ved skæringspunktet, hvor budgettet & mand-dage begrænsninger, der er aktive., Dette betyder, at det punkt, hvor ligningerne + + 2Y 100 100 og. + 3Y. 120 skærer hinanden, giver os den optimale løsning.
værdierne for and og Y, som giver den optimale løsning, er ved (60,20).
for at maksimere fortjenesten skal landbrugeren producere hvede og byg i henholdsvis 60 ha og 20 ha jord.,
Den maksimale profit virksomheden vil opnå er,
Max Z = 50 * (60) + 120 * (20)
= US$5400

Bemærk: Alt lærte her er også blevet undervist i et kursus format i dette gratis kursus – Lineær Programmering til Data Science Professionals
Løse Lineære Program ved Hjælp af R
R er en open-source værktøj, der er meget populær blandt de data, som forskere til væsentlige data videnskab opgaver. Det er meget nemt at udføre lineær programmering, og vi kan opnå en optimal løsning i meget få trin. Kom lad os lære.,eksempel: en legetøjsorganisation fremstiller to typer legetøj A og B. Begge legetøj sælges på Rs.25 og Rs.20 henholdsvis. Der er 2000 ressourceenheder til rådighed hver dag, hvorfra legetøjet a kræver 20 enheder, mens legetøj B kræver 12 enheder. Begge disse legetøj kræver en produktionstid på 5 minutter. Den samlede arbejdstid er 9 timer om dagen. Hvad skal produktionsmængden for hvert af rørene være for at maksimere overskuddet?
Her:
den objektive funktion er:
Ma..,Z=25x+20y
hvor x enheder af pipe A
å er enheder af rør B
Begrænsninger:
20x+12y<=2000
5x+5y<=540
Lad os se koden del nu:
Lyd
Derfor fra output, vi kan se, at organisationen skal producere 88 enheder af toy A og 20 enheder af toy B og den maksimale profit organisation, der vil være Rs.2600.,
Løse Lineære Program ved hjælp af OpenSolver
I virkeligheden, en lineær program kan indeholde 30 til 1000 variabler og løse det enten Grafisk eller Algebraically er næste umuligt. Virksomheder bruger generelt OpenSolver til at tackle disse problemer i den virkelige verden. Her vil jeg tage dig gennem trin for at løse et lineært program ved hjælp af OpenSolver.
OpenSolver er et open-source lineær og optimizer til Microsoft Excel. Det er en avanceret version af en indbygget e .cel Solver. Du kan do .nloade OpenSolver her og følge installationsvejledningen.,
Jeg vil have dig til at få praktisk viden om at bruge OpenSolver. Så for en klar forståelse vil jeg forklare det ved hjælp af et eksempel.eksempel: nedenfor er der et diætdiagram, der giver mig kalorier, protein, kulhydrat og fedtindhold til 4 fødevarer. Sara ønsker en kost med minimale omkostninger., The diet chart is as follows:
| Food Item 1 | Food Item 2 | Food Item 3 | Food Item 4 | |
| Calories | 400 | 200 | 150 | 500 |
| Protien (in grams) | 3 | 2 | 0 | 0 |
| Carbohydrates ( in grams) | 2 | 2 | 4 | 4 |
| Fat (in grams) | 2 | 4 | 1 | 5 |
| Cost | $0.50 | $0.20 | $0.,30 | $0.80 |
diagrammet giver det næringsstof indhold samt per-enhed omkostninger for hver fødevare. Kosten skal planlægges på en sådan måde, at den skal indeholde mindst 500 kalorier, 6 gram protein, 10 gram kulhydrater og 8 gram fedt.
løsning: for det første formulerer jeg mit lineære program i et regneark.
- Trin 1: Identificer beslutningsvariablerne. Her er mine beslutningsvariabler madvarer. Tilføj overskrifterne., Til forsøgsformål går vi ind i vilkårlige værdier. Lad os sige, Sara forbruger 3 enheder af fødevarer punkt 1, 0 enhed af fødevarer punkt 2, 1 enhed af fødevarer punkt 3 og 0 enhed af fødevarer punkt 4. Disse kaldes variable celler.

- Trin 2: nu skriver vi vores objektive funktion. For at kosten skal være optimal, skal vi have minimale omkostninger sammen med krævede kalorier, protein, kulhydrat og fedt.

I celle B7:E7 vi tager henvisning til antallet af enheder., Og i celle B8:E8 sætter vi prisen pr.
i celle B10 ønsker vi de samlede omkostninger ved kosten. De samlede omkostninger er givet af sumpproduktet af antallet af enheder spist og PR. Sumprodukt er givet ved = B7*B8+C7*C8+D7*D8 + E7 * E8. Lad os se dette i et regneark.

- Trin 3: Nu, vi vil komme ind på begrænsninger. Kolonne F indeholder i alt kalorier, protein, kulhydrat og fedt., Det samlede antal kalorieindtag i givet af sumprodukt antallet af madvarer spist og kalorieindtaget pr. For celle F13= Sumprodcut($B$7:$F$7, B13:F13). Tilsvarende for andre. Kolonne G giver uligheden, da problemet kræver kalorier, Protein, kulhydrat og fedt til at være mindst 500, 6, 10 og 8 henholdsvis. Kolonne H giver det krævede næringsindhold.

- Trin 4: Nu, vi vil komme ind på det Lineære program i problemløser. Nu, når du har installeret OpenSolver., Når du klikker på fanen Data, til højre vil du se Model. Klik på modellen, og indtast derefter værdierne en efter en. Først vil vi indtaste den objektive funktion,$B10 dvs. i den objektive celle. Vælg Minimer, fordi vi ønsker at minimere kostprisen.

- Trin 5: Indtast nu beslutningsvariablerne i de variable celler.

- Trin 6: Nu, vil vi tilføje begrænsninger. Den første begrænsning er F13.H13. Tilføj alle begrænsninger en efter en.,
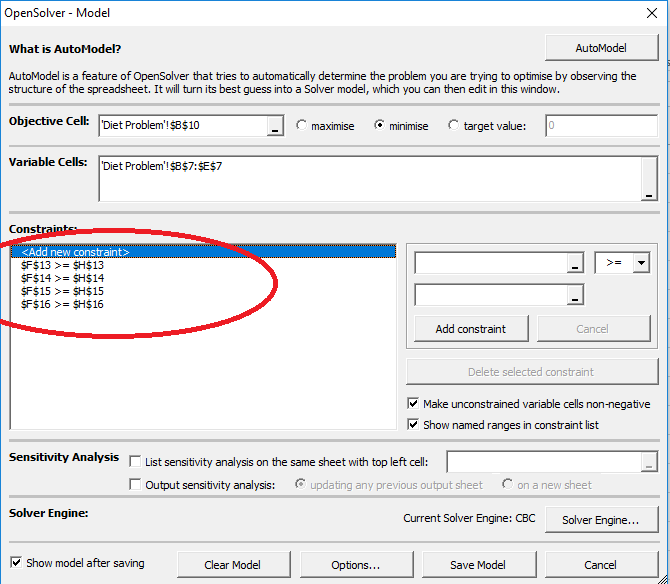
- Trin 7: Nu skal du indtaste en vigtig begrænsning. Den ikke-negativitet begrænsning. Alle beslutningsvariablerne vil være større end 0.

- Trin 8: Klik nu på Gem Model for at afslutte modelleringsprocessen. Når du gemmer modellen, vil den se sådan ud.
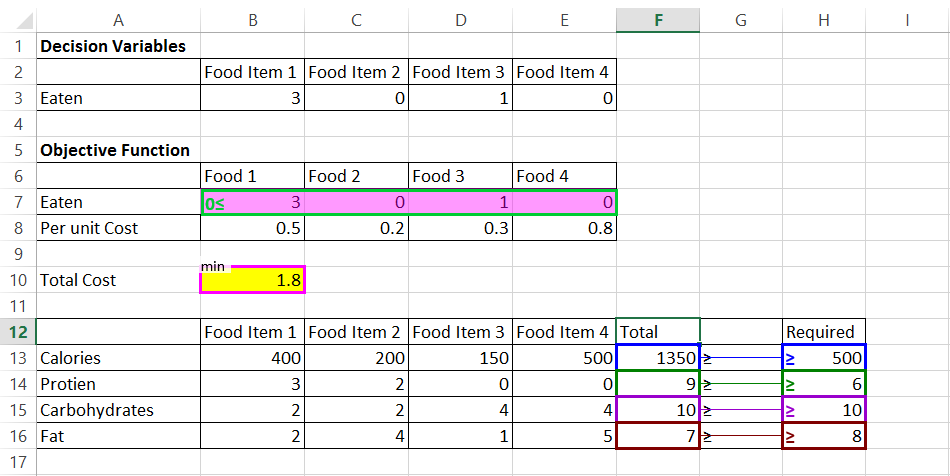
- trin 9: når modellen er gemt, skal du klikke på fanen Data og derefter klikke på løs., Den optimale løsning og værdier vises i de tilsvarende celler. Den optimale minimumspris er US $ 0.90. Sara bør forbruge 3 enheder af fødevaren 2 og 1 enhed af fødevaren 3 for det krævede næringsindhold til minimumsprisen. Dette løser vores lineære program.

Simplex-Metode
Simplex-Metoden er en af de mest magtfulde & populære metoder til lineær programmering. Simple. – metoden er en iterativ procedure for at få den mest gennemførlige løsning., I denne metode fortsætter vi med at omdanne værdien af grundlæggende variabler for at få maksimal værdi for den objektive funktion.
en lineær programmeringsfunktion er i sin standardform, hvis den søger at maksimere den objektive funktion.  underlagt begrænsninger,
underlagt begrænsninger,

. . . . . .
. . . . . .

hvor ![]() og
og ![]() ., Når du tilføjer slack-variable, er den tilsvarende system af tvang ligning er,
., Når du tilføjer slack-variable, er den tilsvarende system af tvang ligning er,
![]()
![]()
. . . .
![]() hvor
hvor ![]()
De variabler,![]()
![]() ……………….
……………….![]() kaldes slack variabler. De er ikke-negative tal, der tilføjes for at fjerne ulighederne fra en ligning.
kaldes slack variabler. De er ikke-negative tal, der tilføjes for at fjerne ulighederne fra en ligning.
ovenstående forklaring giver den teoretiske forklaring af simplex-metoden., Nu skal jeg forklare, hvordan man bruger simple. – metoden i det virkelige liv ved hjælp af E .cel.
eksempel: reklamealternativerne for et firma inkluderer tv -, avis-og radioannoncer. Omkostningerne for hvert medium med publikumsdækning er angivet nedenfor.,
| Television | Newspaper | Radio | |
| Cost per advertisement ($) | 2000 | 600 | 300 |
| Audience per advertisement | 100,000 | 40,000 | 18,000 |
The local newspaper limits the number of advertisements from a single company to ten., For at afbalancere reklamen blandt de tre medietyper skal der desuden ikke forekomme mere end halvdelen af det samlede antal annoncer på radioen. Og mindst 10% skal forekomme på TV. Det ugentlige annonceringsbudget er $ 18.200. Hvor mange annoncer skal køres i hver af de tre typer medier for at maksimere det samlede publikum?
løsning: først vil jeg formulere mit problem for en klar forståelse.,
Trin 1: Identificere Beslutning Variabler
Lad ![]()
![]()
![]() repræsenterer det samlede antal af annoncer, tv, avis og radio hhv.
repræsenterer det samlede antal af annoncer, tv, avis og radio hhv.
Trin 2: objektiv funktion
formålet med virksomheden er at maksimere publikum. Den objektive funktion er givet ved:
![]()
Trin 3: Skriv begrænsningerne
nu vil jeg nævne hver begrænsning en efter en.
det er klart givet, at vi har en budgetbegrænsning., Det samlede budget, der kan tildeles, er $18.200. Og de individuelle omkostninger pr tv, avis og radio reklame er $ 2000, $ 600 og $ 300 henholdsvis. Dette kan være repræsenteret af den ligning,
![]()
For en avisannonce, der er en øvre grænse for antallet af reklamer til 10. Min første begrænsninger er, ![]()
næste begrænsning er antallet af reklamer på tv., Virksomheden ønsker, at mindst 10% af de samlede reklamer skal være på TV. Så, det kan være repræsenteret som:
![]()
Den sidste begrænsning er antallet af reklamer i radio kan ikke være mere end halvdelen af det samlede antal reklamer. Det kan repræsenteres som
![]()
nu har jeg formuleret mit lineære programmeringsproblem. Vi bruger simple. – metoden til at løse dette. Jeg vil tage dig gennem simple. – metoden en efter en.
for at gentage alle begrænsninger er som følger., I have simplified the last two equations to bring them in standard form.
![]()
![]()
![]()
![]()
We have a total of 4 equations. To balance out each equation, I am introducing 4 slack variables,![]()
![]() ,
, ![]() and
and ![]() .,
.,
Så vores ligninger er som følger:
![]()
![]()
![]()
![]()
Jeg håber, at du nu er til rådighed for at gøre følelse af det hele reklame problem. Alle ovenstående ligninger er kun for din bedre forståelse. Nu, hvis du løser disse ligninger, får du værdierne For11= 4, .2= 10 og .3= 14.
når du løser den objektive funktion, får du det maksimale ugentlige publikum som 1,052,000., Du kan følge vejledningen her for at løse ligningen. Følg denne vejledning for at løse et lineært program i e .cel.
Nordvestlige Hjørne Metode og Mindst Omkostninger Metode
6.1 Nordvestlige Hjørne Metode
Det nordvestlige hjørne metode er en særlig type metode, der anvendes til transport problemer i lineær programmering. Det bruges til at beregne den mulige løsning til transport af varer fra et sted til et andet. Når du får et problem i den virkelige verden, som involverer udbud og efterspørgsel fra en kilde til forskellige kilder., De data, modellen omfatter følgende:
- omfanget af udbud og efterspørgsel på hver kilde er givet
- enhed transport af en vare fra hver enkelt kilde til hver destination
modellen forudsætter, at der er kun én vare. Efterspørgslen efter, som kan komme fra forskellige kilder. Målet er at opfylde den samlede efterspørgsel med minimale transportomkostninger. Modellen er baseret på hypotesen om, at den samlede efterspørgsel er lig med det samlede udbud, dvs.modellen er afbalanceret. Lad os forstå dette ved hjælp af et eksempel.,
eksempel: overvej, at der er 3 siloer, der er nødvendige for at imødekomme efterspørgslen fra 4 Møller. (En silo er et lagerområde på gården, der bruges til at opbevare korn, og møllen er en slibefabrik til korn).

Løsning: Lad os forstå, hvad den ovenstående tabel forklarer.
omkostningerne ved transport fra Silo i til Mølle j er givet af omkostningerne i hver celle svarende til udbuddet fra hver silo 1 og efterspørgslen på hver Mølle., For eksempel er omkostningerne ved transport fra Silo 1 til Mill 1 $10, fra Silo 3 til Mill 5 er $18. Det er også givet den samlede efterspørgsel & forsyning til mølle og siloer. Målet er at finde de minimale transportomkostninger, så efterspørgslen efter alle møller er opfyldt.
som navnet antyder North .est corner metode er en metode til tildeling af enhederne startende fra den øverste venstre celle. Efterspørgslen efter Mølle 1 er 5, og Silo 1 har et samlet udbud på 15. Så 5 enheder kan tildeles til Mill1 til en pris på $ 10 pr. Efterspørgslen efter Mill1 er opfyldt., så flytter vi til den øverste venstre celle i Mill 2. Efterspørgslen efter Mill 2 er 15 enheder, som det kan få 10 enheder fra Silo 1 til en pris af $2 per enhed og 5 enheder fra Silo 2 til en pris af $7 per enhed. Så går vi videre til Mill 3, den nordvestlige celle er S2M3. Efterspørgslen efter Mill 3 er 15 enheder, som den kan få fra Silo 2 til en pris af $9 pr. Ved at gå videre til den sidste mølle har Mølle 4 en efterspørgsel på 15 enheder. Det vil få 5 enheder fra en Silo 2 til en pris af $20 per enhed og 10 enheder fra Silo 3 til en pris af $18 per enhed.,
De samlede omkostninger ved transport er = 5*10+(2*10+7*5)+9*15+(20*5+18*10) = $520

6.2 Least Cost Metode
Least Cost-metoden er en anden metode til at beregne den mest rimelige løsning til en lineær programmering problem. Denne metode udleder mere præcise resultater end North .est corner metode. Det bruges til transport og fremstilling problemer. For at holde det enkelt forklarer jeg ovenstående transportproblem.,

ifølge den mindste omkostningsmetode starter du fra cellen, der indeholder de mindste enhedsomkostninger til transport. Så for ovenstående problem leverer jeg 5 enheder fra Silo 3 til en pris pr. Efterspørgslen efter Mill1 er opfyldt. Til mølle 2, Vi leverer 15 enheder fra Silo 1 til en PR pris på $2. Så for Mill 3 Vi leverer 15 enheder fra Silo 2 til en per – enhed pris på $ 9. Så for Mill 4 Vi leverer 10 enheder fra Silo 2 til en per enhed pris på $ 20 og 5 enheder fra Silo 3 en $ 18 per enhed., De samlede transportomkostninger er $ 475.
nå, ovenstående metode forklarer, at vi kan optimere vores omkostninger yderligere med den bedste metode. Lad os tjekke dette ved hjælp af E .cel Solver. Solver er en indbygget add – on i Microsoft e .cel. Det er et tilføjelsesstik, der er tilgængeligt i E .cel. Gå til fil->indstillinger->add-ins->vælg solver->klik på manage->vælg solver->klik på Ok. Din solver er nu tilføjet i e .cel. Du kan tjekke det under fanen Data.,
det første jeg skal gøre er at indtaste mine data i e .cel. Efter indtastning af dataene i e .cel har jeg beregnet summen af C3:F3. Tilsvarende for andre. Dette gøres for at tage den samlede efterspørgsel fra Silo 1 og andre.

Efter dette, jeg mig gonna break my model i to. Den første tabel giver mig de leverede enheder, og den anden tabel giver mig enhedsomkostningerne.,

Nu skal jeg beregne min samlede omkostninger, som vil blive givet ved Sumproduct af enhedsomkostninger og leverede enheder.

Nu er jeg nok bruge Problemløser til at beregne min model. Ligner ovenstående metode. Tilføj den objektive funktion, variable celler, begrænsninger.

Nu din model er klar til at blive løst. Klik på løs, så får du din optimale pris., Den mindste transportomkostninger er $ 435.

Programmer af Lineær Programmering
Lineær programmering og Optimering er brugt i mange forskellige industrier. Fremstillings-og servicebranchen bruger lineær programmering regelmæssigt. I dette afsnit skal vi se på de forskellige anvendelser af lineær programmering.
- fremstillingsindustrier bruger lineær programmering til analyse af deres forsyningskædeoperationer. Deres motiv er at maksimere effektiviteten med minimale driftsomkostninger., I henhold til anbefalingerne fra den lineære programmeringsmodel kan producenten omkonfigurere deres lagringslayout, justere deres arbejdsstyrke og reducere flaskehalse. Her er et lille lager casestudie af Cefterfølgende et amerikansk firma, se denne video for en mere klar forståelse.
- lineær programmering bruges også i organiseret detailhandel til optimering af hyldeplads. Da antallet af produkter på markedet er steget i Spring og grænser, er det vigtigt at forstå, hvad kunden ønsker., Optimering bruges aggressivt i butikker som .almart, Hypercity, Reliance, Big Ba .aar osv. Produkterne i butikken placeres strategisk under hensyntagen til kundens shoppingmønster. Målet er at gøre det nemt for en kunde at finde & vælg de rigtige produkter. Dette er underlagt begrænsninger som begrænset hyldeplads, en række produkter osv.
- optimering bruges også til at optimere leveringsruter. Dette er en udvidelse af det populære rejsesælgerproblem., Servicebranchen bruger optimering til at finde den bedste rute for flere sælgere, der rejser til flere byer. Ved hjælp af klyngedannelse og grådig algoritme afgøres leveringsruterne af virksomheder som fede., Ama .on osv. Målet er at minimere driftsomkostninger og tid.
- optimeringer bruges også i maskinindlæring. Overvåget læring arbejder på det grundlæggende i lineær programmering. Et system er uddannet til at passe på en matematisk model af en funktion fra de mærkede input data, der kan forudsige værdier fra en ukendt testdata.,
nå slutter applikationerne af lineær programmering ikke her. Der er mange flere anvendelser af lineær programmering i den virkelige verden som anvendt af aktionærer, Sport, aktiemarkeder mv. Gå på og udforske yderligere.
End Notes
jeg håber du nød at læse denne artikel. Jeg har forsøgt at forklare alle de grundlæggende begreber under lineær programmering. Hvis du er i tvivl eller spørgsmål, er du velkommen til at sende dem i kommentarfeltet., For nem forståelse har vi brudt denne lange artikel i et kortere kursusformat-Lineær Programmering for data Science Professionals
jeg har forklaret hvert koncept med et ægte eksempel. Jeg vil have dig til at prøve dem i din ende og få praktisk oplevelse. Lad mig vide hvad du synes!
Lær, konkurrere, hack og få ansat!
du kan også læse denne artikel på vores mobilapp
