Einführung
Optimierung ist die Lebensweise. Wir alle haben endliche Ressourcen und Zeit und wollen das Beste daraus machen. Von der produktiven Nutzung Ihrer Zeit bis zur Lösung von Supply-Chain-Problemen für Ihr Unternehmen-alles nutzt Optimierung. Es ist ein besonders interessantes und relevantes Thema in der Datenwissenschaft.,
Es ist auch ein sehr interessantes Thema – es beginnt mit einfachen Problemen, kann aber sehr komplex werden. Zum Beispiel ist das Teilen einer Tafel Schokolade zwischen Geschwistern ein einfaches Optimierungsproblem. Wir denken nicht mathematisch, während wir es lösen. Andererseits kann die Entwicklung einer Bestands-und Lagerstrategie für einen E-Tailer sehr komplex sein. Millionen von SKUs mit unterschiedlicher Popularität in verschiedenen Regionen in definierten Zeit und Ressourcen geliefert werden-Sie sehen, was ich meine!,
Die lineare Programmierung (LP) ist eine der einfachsten Möglichkeiten zur Optimierung. Es hilft Ihnen, einige sehr komplexe Optimierungsprobleme zu lösen, indem Sie einige vereinfachende Annahmen treffen. Als Analyst müssen Sie auf Anwendungen und Probleme stoßen, die durch lineare Programmierung gelöst werden müssen.
Aus irgendeinem Grund erhält LP beim Erlernen der Data Science nicht so viel Aufmerksamkeit, wie es verdient. Also, ich dachte, lass mich dieser großartigen Technik gerecht werden. Ich beschloss, einen Artikel zu schreiben, die lineare Programmierung in einfachem Englisch erklärt., Ich habe den Inhalt so einfach wie möglich gehalten. Die Idee ist, Sie für die lineare Programmierung zu begeistern.
Hinweis-Wenn Sie dies in einem Kursformat lernen möchten, haben wir diesen kostenlosen Kurs für Sie kuratiert-Lineare Programmierung für Datenwissenschaftler
Inhaltsverzeichnis
- Was ist lineare Programmierung?,
- Grundlegende Terminologien
- Der Prozess zur Definition eines LP-Problems
- Lösen Sie lineares Programm mit grafischer Methode
- Lösen Sie lineares Programm mit R
- Lösen Sie lineares Programm mit OpenSolver
- Simplex-Methode
- Northwest Corner-Methode und Methode mit den geringsten Kosten
- Anwendungen der linearen Programmierung
Was ist lineare Programmierung?
Was ist nun lineare Programmierung? Lineare Programmierung ist eine einfache Technik, bei der wir komplexe Beziehungen durch lineare Funktionen darstellen und dann die optimalen Punkte finden., Das wichtige Wort im vorherigen Satz ist dargestellt. Die realen Beziehungen könnten viel komplexer sein – aber wir können sie zu linearen Beziehungen vereinfachen.
Anwendungen der linearen Programmierung sind überall um Sie herum. Sie verwenden lineare Programmierung an persönlichen und beruflichen Fronten. Sie verwenden lineare Programmierung, wenn Sie von zu Hause zur Arbeit fahren und den kürzesten Weg nehmen möchten. Oder wenn Sie eine Projektlieferung haben, machen Sie Strategien, damit Ihr Team effizient für die pünktliche Lieferung arbeitet.,
Beispiel für ein lineares Programmierproblem
Angenommen, ein FedEx-Zusteller hat 6 Pakete an einem Tag zu liefern. Das Lager befindet sich am Punkt A. Die 6 Lieferziele sind durch U, V, W, X, Y und Z. Die Zahlen auf den Linien geben den Abstand zwischen den Städten an. Um Kraftstoff und Zeit zu sparen, möchte der Zusteller den kürzesten Weg nehmen.
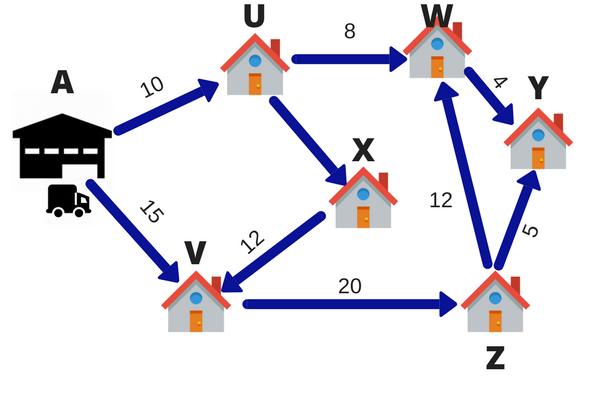
Der Zusteller berechnet also verschiedene Routen, um zu allen 6 Zielen zu gelangen und dann den kürzesten Weg zu finden., Diese Technik der Auswahl des kürzesten Weges wird als lineare Programmierung bezeichnet.
In diesem Fall ist es das Ziel des Zustellers, das Paket an allen 6-Zielen pünktlich zu liefern. Der Prozess der Auswahl der besten Route wird als Operationsforschung bezeichnet. Operationsforschung ist ein Ansatz zur Entscheidungsfindung, der eine Reihe von Methoden zum Betrieb eines Systems umfasst. Im obigen Beispiel war mein System das Liefermodell.
Lineare Programmierung wird verwendet, um die optimale Lösung für ein Problem mit gegebenen Einschränkungen zu erhalten., In der linearen Programmierung formulieren wir unser reales Problem in ein mathematisches Modell. Es handelt sich um eine objektive Funktion, lineare Ungleichungen mit Einschränkungen.
Ist die lineare Darstellung der oben genannten 6 Punkte repräsentativ für die reale Welt? Ja und Nein. Es ist eine zu starke Vereinfachung, da die eigentliche Route keine gerade Linie wäre. Es würde wahrscheinlich mehrere Kurven, Kurven, Signale und Staus haben. Aber mit einer einfachen Annahme haben wir die Komplexität des Problems drastisch reduziert und schaffen eine Lösung, die in den meisten Szenarien funktionieren sollte.,
Ein Problem formulieren-Lassen Sie uns einige Pralinen herstellen
Beispiel: Betrachten Sie ein Schokoladenherstellungsunternehmen, das nur zwei Schokoladensorten herstellt – A und B. Sowohl die Pralinen benötigen nur Milch als auch Choco. Für die Herstellung jeder Einheit von A und B sind folgende Mengen erforderlich:
- Jede Einheit von A benötigt 1 Einheit Milch und 3 Einheiten Choco
- Jede Einheit von B benötigt 1 Einheit Milch und 2 Einheiten Choco
Die Unternehmensküche verfügt über insgesamt 5 Einheiten Milch und 12 Einheiten Choco., Bei jedem Verkauf erzielt das Unternehmen einen Gewinn von
- Rs 6 pro verkaufter Einheit A
- Rs 5 pro verkaufter Einheit B.
Nun möchte das Unternehmen seinen Gewinn maximieren. Wie viele Einheiten von A und B sollte es jeweils produzieren?
Lösung: Das erste, was ich tun werde, ist, das Problem zum besseren Verständnis tabellarisch darzustellen.,>
Lassen Sie die Gesamtzahl der produzierten Einheiten durch Eine be = X
Lassen Sie die Gesamtzahl der produzierten Einheiten von B = Y
Jetzt der gesamte Gewinn wird vertreten durch Z
Der gesamte Gewinn macht das Unternehmen wird durch die Gesamtzahl der Einheiten von A und B erzeugt, multipliziert mit seiner pro-Einheit-Gewinn von Rs 6 und Rs 5 beziehungsweise.,
Profit: Max Z = 6X+5Y
was bedeutet, dass wir maximieren müssen Z.
Das Unternehmen wird versuchen, so viele Einheiten von A und B zu produzieren, um den Gewinn zu maximieren. Aber die Ressourcen Milch und Choco sind in einer begrenzten Menge verfügbar.
Gemäß der obigen Tabelle benötigt jede Einheit von A und B 1 Einheit Milch. Die Gesamtmenge der verfügbaren Milch beträgt 5 Einheiten., Um dies mathematisch darzustellen,
X+Y ≤ 5
Außerdem benötigt jede Einheit von A und B 3 Einheiten & jeweils 2 Einheiten Choco. Die Gesamtmenge der verfügbaren Choco beträgt 12 Einheiten. Um dies mathematisch darzustellen,
3X+2Y ≤ 12
Außerdem können die Werte für Einheiten von A nur ganze Zahlen sein.,
Wir haben also zwei weitere Einschränkungen: X ≥ 0 & Y ≥ 0
Um maximalen Gewinn zu erzielen, müssen die oben genannten Ungleichungen erfüllt sein.
Dies nennt man die Formulierung eines realen Problems in ein mathematisches Modell.
Allgemeine Terminologien, die in der linearen Programmierung verwendet werden
Definieren wir einige Terminologien, die in der linearen Programmierung verwendet werden, im obigen Beispiel.
- Entscheidungsvariablen: Die Entscheidungsvariablen sind die Variablen, die meine Ausgabe bestimmen., Sie stellen meine ultimative Lösung dar. Um ein Problem zu lösen, müssen wir zuerst die Entscheidungsvariablen identifizieren. Für das obige Beispiel ist die Gesamtzahl der Einheiten für A und B, die mit X & Y bezeichnet sind, meine Entscheidungsvariablen.
- Zielfunktion: Sie ist definiert als das Ziel, Entscheidungen zu treffen. Im obigen Beispiel möchte das Unternehmen den Gesamtgewinn von Z erhöhen Also, Gewinn ist meine objektive Funktion.,
- Einschränkungen: Die Einschränkungen sind die Einschränkungen oder Einschränkungen für die Entscheidungsvariablen. Sie begrenzen normalerweise den Wert der Entscheidungsvariablen. Im obigen Beispiel sind die Begrenzung der Verfügbarkeit von Ressourcen Milch und Choco meine Einschränkungen.
- Nicht-Negativitätseinschränkung: Bei allen linearen Programmen sollten die Entscheidungsvariablen immer nicht-negative Werte annehmen. Dies bedeutet, dass die Werte für Entscheidungsvariablen größer oder gleich 0 sein sollten.,
Der Prozess zur Formulierung eines linearen Programmierproblems
Lassen Sie uns die Schritte zur generischen Definition eines linearen Programmierproblems betrachten:
- Identifizieren Sie die Entscheidungsvariablen
- Schreiben Sie die Zielfunktion
- Erwähnen Sie die Einschränkungen
- Geben Sie explizit die Nicht-Negativitätseinschränkung
an, damit ein Problem eine lineare Programmieraufgabe ist roblem, die Entscheidungsvariablen, die Zielfunktion und die Einschränkungen müssen alle lineare Funktionen sein.,
Wenn alle drei Bedingungen erfüllt sind, wird dies als lineares Programmierproblem bezeichnet.
Lineare Programme mit grafischer Methode lösen
Ein lineares Programm kann mit mehreren Methoden gelöst werden. In diesem Abschnitt werden wir uns die grafische Methode zum Lösen eines linearen Programms ansehen. Diese Methode wird verwendet, um ein lineares Programm mit zwei Variablen zu lösen. Wenn Sie nur zwei Entscheidungsvariablen haben, sollten Sie die grafische Methode verwenden, um die optimale Lösung zu finden.,
Bei einer grafischen Methode wird eine Reihe linearer Ungleichungen formuliert, die den Einschränkungen unterliegen. Dann werden die Ungleichungen auf einer Xy-Ebene aufgetragen. Sobald wir alle Ungleichungen in einem Diagramm gezeichnet haben, gibt uns der sich kreuzende Bereich eine machbare Region. Die machbare Region erklärt, welche Werte unser Modell annehmen kann. Und es gibt uns auch die optimale Lösung.
Lassen Sie uns dies anhand eines Beispiels verstehen.
Beispiel: Ein Landwirt hat kürzlich ein 110 Hektar großes Grundstück erworben., Er hat beschlossen, Weizen und Gerste auf diesem Land anzubauen. Aufgrund der Qualität der Sonne und des hervorragenden Klimas der Region kann die gesamte Produktion von Weizen und Gerste verkauft werden.,h Sorte in der 110 Hektar, angesichts der Kosten, Nettogewinn und Arbeitsanforderungen nach den unten gezeigten Daten:
| Sorte | Kosten (Preis/Hec) | Nettogewinn (Preis/Hec) | Mann-Tage/Hec |
| Weizen | 100 | 50 | 10 |
| 100 | 200 | 120 | 30 |
Der Landwirt hat ein Budget von US$10.000 und Verfügbarkeit von 1.200 Manntagen während des Planungshorizonts., Finden Sie die optimale Lösung und den optimalen Wert.
Lösung: Um dieses Problem zu lösen, formulieren wir zuerst unser lineares Programm.
Formulierung des linearen Problems
Schritt 1: Identifizieren Sie die Entscheidungsvariablen
Die Gesamtfläche für den Anbau von Weizen = X (in Hektar)
Die Gesamtfläche für den Anbau von Gerste = Y (in Hektar)
X und Y sind meine Entscheidungsvariablen.
Schritt 2: Schreiben Sie die Zielfunktion
Da die Produktion aus dem gesamten Land auf dem Markt verkauft werden kann. Der Landwirt möchte den Gewinn für seine gesamten Produkte maximieren., Wir erhalten sowohl für Weizen als auch für Gerste einen Nettogewinn. Der Landwirt verdient einen Nettogewinn von US $ 50 für jeden Hektar Weizen und US $ 120 für jede Gerste.
Unsere Zielfunktion (gegeben durch Z) ist Max Z = 50X + 120Y
Schritt 3: Schreiben der Einschränkungen
1. Es ist gegeben, dass der Bauer ein Gesamtbudget von US$10,000 hat. Die Kosten für die Erzeugung von Weizen und Gerste pro Hektar werden ebenfalls an uns weitergegeben. Wir haben eine Obergrenze für die Gesamtkosten, die der Landwirt ausgibt. So wird unsere Gleichung wird zu:
100X + 200Y ≤ 10,000
2., Die nächste Einschränkung ist die Obergrenze für die Verfügbarkeit der Gesamtzahl der Arbeitstage für den Planungshorizont. Die Gesamtzahl der verfügbaren Manntage beträgt 1200. Gemäß der Tabelle erhalten wir die Manntage pro Hektar für Weizen und Gerste.
10X + 30Y ≤ 1200
3. Die dritte Einschränkung ist die Gesamtfläche für die Plantage. Die gesamte verfügbare Fläche beträgt 110 Hektar., So wird die Gleichung,
X + Y ≤ 110
Schritt 4: Die Nicht-Negativitätseinschränkung
Die Werte von X und Y sind größer oder gleich 0. Das ist selbstverständlich.
X ≥ 0, Y ≥ 0
Wir haben formuliert, die unser lineares Programm. Es ist Zeit, es zu lösen.
Lösen einer LP durch grafische Methode
Da wir wissen, dass X, Y ≥ 0. Wir werden nur den ersten Quadranten betrachten.
Um für den Graphen für die obigen Gleichungen zu zeichnen, werde ich zuerst alle Gleichungen vereinfachen.,
100X + 200Y ≤ 10,000 kann durch Dividieren durch 100 auf X + 2Y ≤ 100 vereinfacht werden.
10X + 30Y ≤ 1200 kann durch Division durch 10 auf X + 3Y ≤ 120 vereinfacht werden.
Die Dritte Gleichung ist in vereinfachter form, X + Y ≤ 110.
Zeichnen Sie die ersten 2 Zeilen in einem Diagramm im ersten Quadranten (wie unten gezeigt)
Die optimal durchführbare Lösung wird am Schnittpunkt erreicht, an dem die Budget & Man-Days-Einschränkungen aktiv sind., Dies bedeutet, dass der Punkt, an dem sich die Gleichungen X + 2Y ≤ 100 und X + 3Y ≤ 120 schneiden, uns die optimale Lösung gibt.
Die Werte für X und Y, die die optimale Lösung ergeben, liegen bei (60,20).
Um den Gewinn zu maximieren, sollte der Landwirt Weizen und Gerste auf 60 Hektar bzw.,
Der maximale Gewinn, den das Unternehmen erzielen wird, ist
Max Z = 50 * (60) + 120 * (20)
= US$5400

Hinweis: Alles, was hier gelehrt wurde, wurde auch in einem Kursformat in diesem kostenlosen Kurs gelehrt – Lineare Programmierung für Datenwissenschaftler
Lösen Sie lineares Programm mit R
R ist ein Open-Source-Tool, das bei den Datenwissenschaftlern für wichtige datenwissenschaftliche Aufgaben sehr beliebt ist. Die Durchführung der linearen Programmierung ist sehr einfach und wir können in wenigen Schritten eine optimale Lösung erreichen. Komm, lass uns lernen.,
Beispiel: Eine Spielzeugherstellungsorganisation stellt zwei Arten von Spielzeug her A und B. Beide Spielzeuge werden bei Rs verkauft.25 und Rs.20 respectively. Es stehen täglich 2000 Ressourceneinheiten zur Verfügung, von denen das Spielzeug A 20 Einheiten benötigt, während Spielzeug B 12 Einheiten benötigt. Beide Spielzeuge benötigen eine Produktionszeit von 5 Minuten. Die Gesamtarbeitszeit beträgt 9 Stunden pro Tag. Was sollte die Herstellungsmenge für jedes der Rohre sein, um den Gewinn zu maximieren?
Hier:
Die Zielfunktion lautet:
Max.,Z=25x+20y
wobei x die Einheiten von pipe A
y die Einheiten von Pipe B
Einschränkungen:
20x+12y<=2000
5x+5y<=540
Sehen wir uns jetzt den Codeteil an:
Output
Daher sehen wir aus der Ausgabe, dass die Organisation 88 Einheiten Spielzeug A und 20 Einheiten Spielzeug B produzieren sollte und der maximale Gewinn für die Organisation Rs sein wird.2600.,
Lösen Sie lineares Programm mit OpenSolver
In Wirklichkeit kann ein lineares Programm 30 bis 1000 Variablen enthalten und es entweder grafisch oder algebraisch lösen ist fast unmöglich. Unternehmen verwenden im Allgemeinen OpenSolver, um diese realen Probleme anzugehen. Hier führe ich Sie durch Schritte, um ein lineares Programm mit OpenSolver zu lösen.
OpenSolver ist ein Open-Source-Tool und Optimierer für Microsoft Excel. Es ist eine erweiterte Version eines integrierten Excel-Löser. Sie können OpenSolver hier herunterladen und dem Installationshandbuch folgen.,
Ich möchte, dass Sie praktische Kenntnisse über die Verwendung von OpenSolver erhalten. Für ein klares Verständnis werde ich es anhand eines Beispiels erklären.
Beispiel: Unten gibt es eine Diätkarte, die mir Kalorien, Eiweiß, Kohlenhydrate und Fettgehalt für 4 Lebensmittel gibt. Sara will eine Diät mit minimalen Kosten., The diet chart is as follows:
| Food Item 1 | Food Item 2 | Food Item 3 | Food Item 4 | |
| Calories | 400 | 200 | 150 | 500 |
| Protien (in grams) | 3 | 2 | 0 | 0 |
| Carbohydrates ( in grams) | 2 | 2 | 4 | 4 |
| Fat (in grams) | 2 | 4 | 1 | 5 |
| Cost | $0.50 | $0.20 | $0.,30 | $ 0.80 |
Das Diagramm gibt den Nährstoffgehalt sowie die Kosten pro Einheit für jedes Lebensmittel an. Die Diät muss so geplant werden, dass sie mindestens 500 Kalorien, 6 Gramm Protein, 10 Gramm Kohlenhydrate und 8 Gramm Fett enthalten sollte.
Lösung: Zuerst werde ich mein lineares Programm in einer Tabelle formulieren.
- Schritt 1: Identifizieren Sie die Entscheidung Variablen. Hier sind meine Entscheidungsvariablen die Lebensmittel. Fügen Sie die Header hinzu., Zu Testzwecken geben wir beliebige Werte ein. Angenommen, Sara verbraucht 3 Einheiten Lebensmittel 1, 0 Einheit Lebensmittel 2, 1 Einheit Lebensmittel 3 und 0 Einheit Lebensmittel 4. Diese werden variable Zellen genannt.

- Schritt 2: Jetzt schreiben wir unser Ziel-Funktion. Damit die Ernährung optimal ist, müssen wir minimale Kosten zusammen mit den erforderlichen Kalorien, Eiweiß, Kohlenhydraten und Fett haben.

In Zelle B7:E7 nehmen wir den Verweis auf die Anzahl der Einheiten., Und in Zelle B8: E8 legen wir die Kosten pro Einheit für jedes Lebensmittel fest.
In Zelle B10 möchten wir die Gesamtkosten der Diät. Die Gesamtkosten werden durch den Sumpf GEGEBENPRODUKT der Anzahl der Einheiten gegessen und pro Stück Kosten. Der Sumproduct-Funktion ist gegeben durch = B7*B8+C7*C8+D7*D8+E7*E8. Lassen Sie uns dies in einer Tabelle sehen.

- Schritt 3: Jetzt, wir werden geben Sie die Zwangsbedingungen. Spalte F enthält insgesamt Kalorien, Eiweiß, Kohlenhydrate und Fett., Die Gesamtzahl der Kalorienzufuhr in gegeben durch sumprodukt die Anzahl der Lebensmittel gegessen und die Kalorien pro Lebensmittel verbraucht. Für die Zelle F13= Sumprodcut($B$7:$F$7, B13:F13). Ähnlich für andere. Spalte G gibt die Ungleichheit an, da das Problem erfordert, dass Kalorien, Eiweiß, Kohlenhydrate und Fett mindestens 500, 6, 10 bzw. Spalte H gibt den erforderlichen Nährstoffgehalt an.

- Schritt 4: Jetzt, wir werden geben Sie das Lineare Programm in den solver. Nun, sobald Sie OpenSolver installiert haben., Wenn Sie auf die Registerkarte Daten klicken, sehen Sie rechts Modell. Klicken Sie auf das Modell und geben Sie die Werte einzeln ein. Zuerst geben wir die Zielfunktion$B10 dh in die Zielzelle ein. Wählen Sie Minimieren, weil wir die Diätkosten minimieren möchten.

- Schritt 5: geben Sie Nun die Entscheidung Variablen in die Variablen Zellen.

- 6. Schritt: Nun fügen wir die Einschränkungen. Die erste Einschränkung ist die F13 ≥ H13. Fügen Sie alle Einschränkungen einzeln hinzu.,
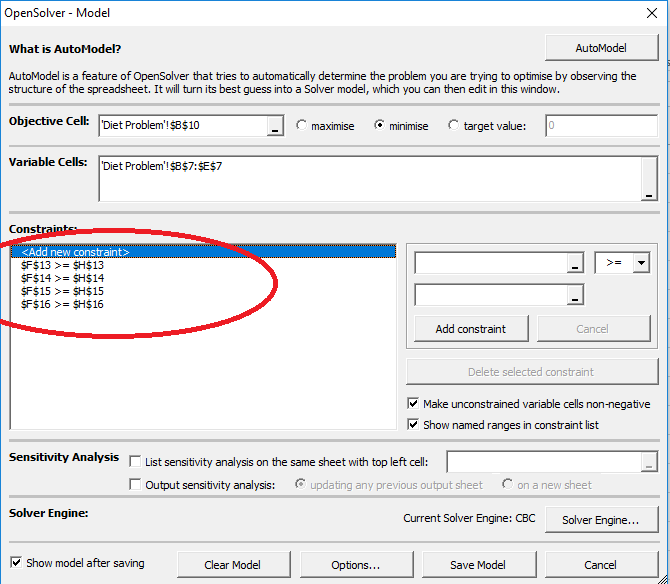
- Schritt 7: Jetzt müssen Sie eine wichtige Einschränkung. Die nicht-Negativität Einschränkung. Alle Entscheidungsvariablen sind größer als 0.

- Schritt 8: Klicken Sie nun auf Modell speichern, um den Modellierungsprozess abzuschließen. Sobald Sie das Modell gespeichert haben, sieht es ungefähr so aus.
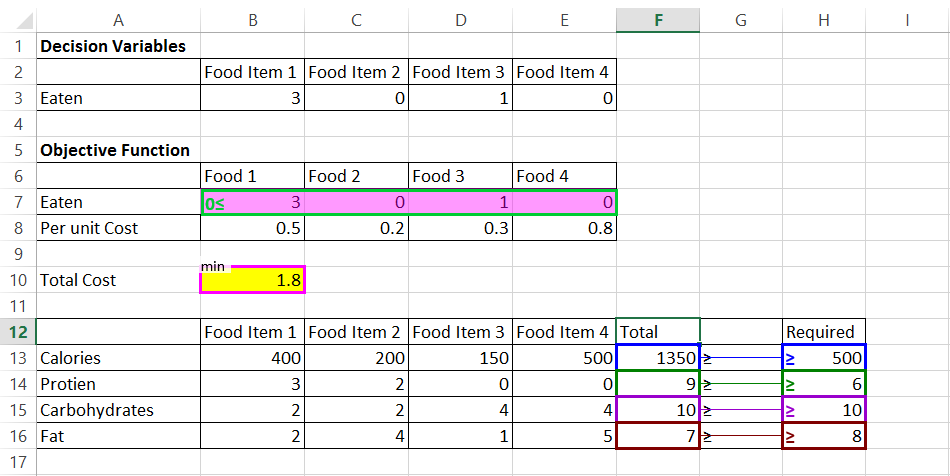
- Schritt 9: Sobald das Modell gespeichert ist, klicken Sie auf die Registerkarte Daten und dann auf Lösen., Die optimale Lösung und Werte werden in den entsprechenden Zellen angezeigt. Die optimalen Mindestkosten betragen US $ 0.90. Sara sollte 3 Einheiten Lebensmittelpunkt 2 und 1 Einheit Lebensmittelpunkt 3 für den erforderlichen Nährstoffgehalt zu minimalen Kosten konsumieren. Dies löst unser lineares Programm.

Simplex-Methode
Simplex-Methode ist eine der mächtigsten & beliebte Methoden für lineare Programmierung. Die Simplex-Methode ist ein iteratives Verfahren, um die bestmögliche Lösung zu erhalten., Bei dieser Methode transformieren wir den Wert grundlegender Variablen weiter, um den Maximalwert für die Zielfunktion zu erhalten.
Eine lineare Programmierfunktion ist in ihrer Standardform, wenn sie versucht, die Zielfunktion zu maximieren.  Einschränkungen vorbehalten,
Einschränkungen vorbehalten,
. . . . . .
. . . . . .

wobei ![]() und
und ![]() ., Nach dem hinzufügen von slack-Variablen, die entsprechenden system der constraint-Gleichung ist,
., Nach dem hinzufügen von slack-Variablen, die entsprechenden system der constraint-Gleichung ist,
![]()
![]()
. . . .
wobei ![]()
Die Variablen![]()
![]() ……………….
……………….![]() werden Slack-Variablen genannt. Sie sind nicht negative Zahlen, die hinzugefügt werden, um die Ungleichungen aus einer Gleichung zu entfernen.
werden Slack-Variablen genannt. Sie sind nicht negative Zahlen, die hinzugefügt werden, um die Ungleichungen aus einer Gleichung zu entfernen.
Die obige Erklärung gibt die theoretische Erklärung der simplex-Methode., Jetzt werde ich erklären, wie man die Simplex-Methode im wirklichen Leben mit Excel verwendet.
Beispiel: Die Werbealternativen für ein Unternehmen umfassen Fernseh -, Zeitungs-und Radiowerbung. Die Kosten für jedes Medium mit seiner Publikumsabdeckung sind unten angegeben.,
| Television | Newspaper | Radio | |
| Cost per advertisement ($) | 2000 | 600 | 300 |
| Audience per advertisement | 100,000 | 40,000 | 18,000 |
The local newspaper limits the number of advertisements from a single company to ten., Darüber hinaus sollte, um die Werbung unter den drei Arten von Medien auszugleichen, nicht mehr als die Hälfte der Gesamtzahl der Anzeigen im Radio auftreten. Und mindestens 10% sollten im Fernsehen auftreten. Das wöchentliche Werbebudget beträgt $ 18,200. Wie viele Anzeigen sollten in jedem der drei Medientypen ausgeführt werden, um das Gesamtpublikum zu maximieren?
Lösung: Zuerst werde ich mein Problem für ein klares Verständnis formulieren.,
Schritt 1: Ermitteln Sie die Entscheidung Variablen
Lassen Sie ![]() ,
,![]() ,
, ![]() repräsentieren die Gesamtzahl der anzeigen, für das Fernsehen, die Zeitung und das radio beziehungsweise.
repräsentieren die Gesamtzahl der anzeigen, für das Fernsehen, die Zeitung und das radio beziehungsweise.
Schritt 2: Zielfunktion
Das Ziel des Unternehmens ist es, das Publikum zu maximieren. Die Zielfunktion ist gegeben durch:
![]()
Schritt 3: Notieren Sie sich die Einschränkungen
Jetzt werde ich jede Einschränkung einzeln erwähnen.
Es ist klar, dass wir eine Budgetbeschränkung haben., Das Gesamtbudget, das zugewiesen werden kann, ist $ 18,200. Und die individuellen Kosten pro Fernsehen, Zeitung und Radio-Werbung ist $2000, $600 und $300 beziehungsweise. Dies kann durch die Gleichung dargestellt werden,
![]()
Für eine Zeitungsanzeige gibt es eine Obergrenze für die Anzahl der Anzeigen auf 10. Meine erste Einschränkungen sind, ![]()
Die nächste Einschränkung ist die Anzahl der anzeigen im Fernsehen., Das Unternehmen möchte, dass mindestens 10% der gesamten Anzeigen im Fernsehen geschaltet werden. Es kann also wie folgt dargestellt werden:
![]()
Die letzte Einschränkung ist, dass die Anzahl der Anzeigen im Radio nicht mehr als die Hälfte der Gesamtzahl der Anzeigen betragen darf. Es kann als
![]()
Jetzt habe ich mein lineares Programmierproblem formuliert. Wir verwenden die Simplex-Methode, um dies zu lösen. Ich werde Sie nacheinander durch die Simplex-Methode führen.
Um alle Einschränkungen zu wiederholen, sind wie folgt., I have simplified the last two equations to bring them in standard form.
![]()
![]()
![]()
![]()
We have a total of 4 equations. To balance out each equation, I am introducing 4 slack variables,![]()
![]() ,
, ![]() and
and ![]() .,
.,
Unsere Gleichungen lauten also wie folgt:
![]()
![]()
![]()
![]()
Ich hoffe, dass Sie jetzt verfügbar sind, um das gesamte Werbeproblem zu verstehen. Alle oben genannten Gleichungen dienen nur zum besseren Verständnis. Wenn Sie nun diese Gleichungen lösen, erhalten Sie die Werte für X1= 4, X2= 10 und X3= 14.
Bei der Lösung der Zielfunktion erhalten Sie das maximale wöchentliche Publikum als 1.052.000., Sie können dem Tutorial hier folgen, um die Gleichung zu lösen. Befolgen Sie dieses Tutorial, um ein lineares Programm in Excel zu lösen.
Northwest Corner Methode und Least-Cost-Methode
6.1 Northwest Corner Methode
northwest corner Methode ist eine Besondere Methode für die Transport-Probleme in der linearen Programmierung. Es wird verwendet, um die machbare Lösung für den Transport von Gütern von einem Ort zum anderen zu berechnen. Wann immer Sie ein reales Problem bekommen, das Angebot und Nachfrage aus einer Quelle verschiedener Quellen umfasst., Das Datenmodell enthält Folgendes:
- Das Niveau von Angebot und Nachfrage an jeder Quelle ist gegeben
- Die Transporteinheit einer Ware von jeder Quelle zu jedem Ziel
Das Modell geht davon aus, dass es nur eine Ware gibt. Die Nachfrage dafür kann aus verschiedenen Quellen kommen. Ziel ist es, den Gesamtbedarf mit minimalen Transportkosten zu decken. Das Modell basiert auf der Hypothese, dass die Gesamtnachfrage gleich dem Gesamtangebot ist, d. h. Das Modell ist ausgeglichen. Lassen Sie uns dies anhand eines Beispiels verstehen.,
Beispiel: Es sind 3 Silos erforderlich, um den Bedarf von 4 Mühlen zu decken. (Ein Silo ist ein Lagerbereich der Farm zur Lagerung von Getreide und Mühle ist eine Mahlfabrik für Getreide).

Lösung: Lassen Sie uns verstehen, was der obigen Tabelle erläutert.
Die Transportkosten von Silo i zu Mühle j ergeben sich aus den Kosten in jeder Zelle, die dem Angebot von jedem Silo 1 und der Nachfrage in jeder Mühle entsprechen., Zum Beispiel betragen die Transportkosten von Silo 1 zu Mühle 1 10 USD, von Silo 3 zu Mühle 5 18 USD. Es ist auch die Gesamtnachfrage gegeben & Angebot für Mühle und Silos. Ziel ist es, die minimalen Transportkosten so zu finden, dass die Nachfrage nach allen Mühlen befriedigt wird.
Wie der Name schon sagt, ist die Eckmethode eine Methode zum Zuweisen der Einheiten ausgehend von der Zelle oben links. Die Nachfrage nach Mühle 1 ist 5 und Silo 1 hat ein Gesamtangebot von 15. So können 5 Einheiten Mill1 zu einem Preis von 10 USD pro Einheit zugewiesen werden. Die Nachfrage nach Mill1 ist erfüllt., dann bewegen wir uns in die obere linke Zelle von Mühle 2. Die Nachfrage nach Mühle 2 beträgt 15 Einheiten, die 10 Einheiten von Silo 1 zu einem Preis von 2 USD pro Einheit und 5 Einheiten von Silo 2 zu einem Preis von 7 USD pro Einheit erhalten können. Dann gehen wir auf Mühle 3, die erste Zelle ist S2M3. Die Nachfrage nach Mühle 3 beträgt 15 Einheiten, die sie von Silo 2 zu einem Preis von 9 USD pro Einheit erhalten kann. Auf dem Weg zur letzten Mühle hat Mühle 4 einen Bedarf von 15 Einheiten. Es wird 5 Einheiten von einem Silo 2 zu einem Preis von $20 pro Einheit und 10 Einheiten von Silo 3 zu einem Preis von $18 pro Einheit erhalten.,
Die Gesamtkosten des Transports sind = 5*10+(2*10+7*5)+9*15+(20*5+18*10) = $520

Die kostengünstigste Methode
Die kostengünstigste Methode ist eine weitere Methode zur Berechnung der am besten durchführbaren Lösung für ein lineares Programmierproblem. Diese Methode leitet genauere Ergebnisse ab als die Nordwest-Eckmethode. Es wird für Transport-und Herstellungsprobleme verwendet. Um es einfach zu halten, erkläre ich das obige Transportproblem.,

Nach der Methode mit den geringsten Kosten beginnen Sie mit der Zelle, die die geringsten Stückkosten für den Transport enthält. Für das obige Problem liefere ich 5 Einheiten von Silo 3 zu einem Stückpreis von 4 US-Dollar. Die Nachfrage nach Mill1 ist erfüllt. Für Mühle 2 liefern wir 15 Einheiten von Silo 1 zu einem Stückpreis von $ 2. Dann liefern wir für Mühle 3 15 Einheiten von Silo 2 zu einem Stückpreis von 9 USD. Dann liefern wir für Mill 4 10 Einheiten von Silo 2 zu einem Stückpreis von 20 USD und 5 Einheiten von Silo 3 zu 18 USD pro Einheit., Die gesamten Transportkosten betragen $475.
Nun, die obige Methode erklärt, dass wir unsere Kosten mit der besten Methode weiter optimieren können. Lassen Sie uns dies mit Excel Solver überprüfen. Solver ist ein integriertes add-on in Microsoft Excel. Es ist ein add-in plug in Excel verfügbar. Gehe zu file->options->add-ins->select solver->click on manage->select solver->klicken Sie auf OK. Ihr Solver wird jetzt in Excel hinzugefügt. Sie können es unter der Registerkarte Daten überprüfen.,
Als erstes werde ich meine Daten in Excel eingeben. Nach Eingabe der Daten in Excel habe ich die Summe von C3:F3 berechnet. Ähnlich für andere. Dies geschieht, um den Gesamtbedarf von Silo 1 und anderen zu decken.

Danach werde ich mein Modell in zwei Teile aufteilen. Die erste Tabelle gibt mir die gelieferten Einheiten und die zweite Tabelle gibt mir die Stückkosten.,

Jetzt berechne ich meine Gesamtkosten, die durch Sumproduct der gelieferten Stückkosten und Einheiten angegeben werden.

Jetzt werde ich Solver verwenden, um mein Modell zu berechnen. Ähnlich wie bei der obigen Methode. Fügen Sie die Zielfunktion, variable Zellen, Einschränkungen hinzu.

Jetzt Ihr Modell bereit ist, gelöst werden. Klicken Sie auf Lösen und Sie erhalten Ihre optimalen Kosten., Die minimale Transport Kosten ist $435.

Anwendungen der linearen Programmierung
Lineare Programmierung und Optimierung werden in verschiedenen Branchen eingesetzt. Die Fertigungs-und Dienstleistungsindustrie verwendet regelmäßig lineare Programmierung. In diesem Abschnitt werden wir uns die verschiedenen Anwendungen der linearen Programmierung ansehen.
- Die Fertigungsindustrie verwendet lineare Programmierung zur Analyse ihrer Lieferkettenoperationen. Ihr Motiv ist es, die Effizienz bei minimalen Betriebskosten zu maximieren., Gemäß den Empfehlungen aus dem linearen Programmiermodell kann der Hersteller sein Speicherlayout neu konfigurieren, seine Belegschaft anpassen und die Engpässe reduzieren. Hier ist ein kleines Lager Fallstudie von Cequent ein US-Unternehmen, sehen Sie dieses Video für ein klareres Verständnis.
- Die lineare Programmierung wird auch im organisierten Einzelhandel zur Optimierung der Regalfläche verwendet. Da die Anzahl der Produkte auf dem Markt sprunghaft zugenommen hat, ist es wichtig zu verstehen, was der Kunde will., Optimierung wird aggressiv in Geschäften wie Walmart, Hypercity, Reliance, Big Bazaar usw. eingesetzt. Die Produkte im Geschäft werden strategisch unter Berücksichtigung des Kundeneinkaufsmusters platziert. Ziel ist es, es einem Kunden leicht zu machen, & die richtigen Produkte auszuwählen. Dies unterliegt Einschränkungen wie begrenzter Regalfläche,einer Vielzahl von Produkten usw.
- Die Optimierung wird auch zur Optimierung von Lieferwegen verwendet. Dies ist eine Erweiterung des beliebten travelling salesman problem., Die Dienstleistungsbranche nutzt die Optimierung, um die beste Route für mehrere Verkäufer zu finden, die in mehrere Städte reisen. Mit Hilfe von Clustering und Greedy-Algorithmus werden die Lieferwege von Unternehmen wie FedEx, Amazon usw. festgelegt. Ziel ist es, die Betriebskosten und-zeit zu minimieren.
- Optimierungen werden auch im maschinellen Lernen verwendet. Überwachtes Lernen arbeitet an den Grundlagen der linearen Programmierung. Ein System wird so trainiert, dass es auf ein mathematisches Modell einer Funktion aus den beschrifteten Eingabedaten passt, die Werte aus unbekannten Testdaten vorhersagen können.,
Nun, die Anwendungen der linearen Programmierung enden hier nicht. Es gibt viele weitere Anwendungen der linearen Programmierung in der realen Welt, wie sie von Aktionären, Sport, Aktienmärkten usw. angewendet werden. Gehen Sie weiter und erkunden Sie weiter.
Endnotizen
Ich hoffe, es hat Ihnen Spaß gemacht, diesen Artikel zu lesen. Ich habe versucht, alle grundlegenden Konzepte unter linearer Programmierung zu erklären. Wenn Sie Zweifel oder Fragen haben, können Sie diese gerne im Kommentarbereich posten., Zum besseren Verständnis haben wir diesen langen Artikel in ein kürzeres Kursformat unterteilt-Lineare Programmierung für Datenwissenschaftler
Ich habe jedes Konzept mit einem realen Beispiel erklärt. Ich möchte, dass Sie sie an Ihrem Ende ausprobieren und praktische Erfahrungen sammeln. Lass mich wissen, was du denkst!
Lernen, zu konkurrieren, zu hacken und bekommen angeheuert!
Sie können diesen Artikel auch in unserer mobilen APP lesen 
